03.02. Линейные операции над векторами
Линейными операциями над векторами называют сложение, вычитание, умножение вектора на число.
Суммой векторов Называют третий вектор
Называют третий вектор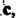 Начало которого совпадает с началом вектора
Начало которого совпадает с началом вектора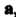 , а конец - с концом вектора
, а конец - с концом вектора При условии, что вектор
При условии, что вектор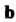 Отложен из конца вектора
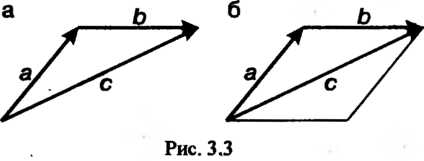
Отложен из конца вектора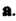 Вектор с получается по правилу треугольника (рис. 3.3, а) или параллелограмма (рис. 3.3, б).
Вектор с получается по правилу треугольника (рис. 3.3, а) или параллелограмма (рис. 3.3, б).
Аналогично определяется сумма трех и более векторов. Суммой и векторов 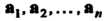 Называется вектор, начало которого совпадает с началом первого вектора
Называется вектор, начало которого совпадает с началом первого вектора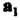 , конец - с концом последнего
, конец - с концом последнего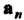 При условии, что каждый последующий вектор
При условии, что каждый последующий вектор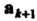 Отложен из конца предыдущего
Отложен из конца предыдущего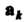
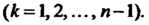 Указанный способ построения суммы называется правилом замыкающей.
Указанный способ построения суммы называется правилом замыкающей.
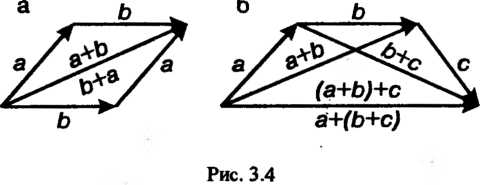
Сумма векторов обладает свойством переместительности (коммутативности, рис. 3.4):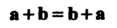
И свойством сочетательности (ассоциативности) 
Сумма трех некомпланарных векторов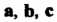 Наряду с правилом замыкающей по
Наряду с правилом замыкающей по
Лучается и по правилу параллелепипеда: сумма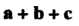 Равна вектору
Равна вектору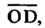 Где
Где
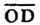 - диагональ параллелепипеда, построенного на векторах
- диагональ параллелепипеда, построенного на векторах
 , отложенных из одной точки (рис. 3.5).
, отложенных из одной точки (рис. 3.5).
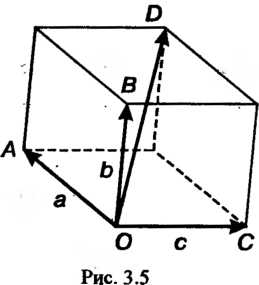

Из определения суммы следует, что

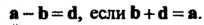
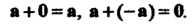
Разностью Двух векторов
Двух векторов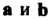 Называется такой вектор
Называется такой вектор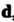 , который в
, который в
Сумме с вектором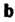 Дает вектор
Дает вектор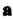 :
:
Чтобы получить разность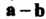 Двух векторов
Двух векторов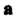 И
И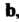 Необходимо отложить их из одной точки и соединить конец второго вектора с концом первого (рис. 3.6, а).
Необходимо отложить их из одной точки и соединить конец второго вектора с концом первого (рис. 3.6, а).
Разность Равна сумме двух векторов
Равна сумме двух векторов И
И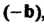 , где
, где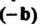 - вектор, противоположный вектору
- вектор, противоположный вектору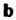 (рис! 3.6, б), т. е.
(рис! 3.6, б), т. е.
Векторы — диагонали параллелограмма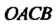 (рис. 3.6, в), построенного на векторах
(рис. 3.6, в), построенного на векторах Являются соответственно суммой и разностью этих векторов.
Являются соответственно суммой и разностью этих векторов.


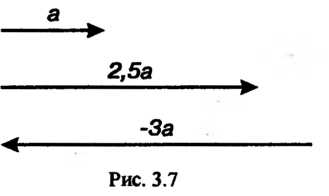
Произведением вектора а на число а называется вектор 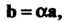
Удовлетворяющий условиям: 1)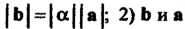 Одинаково направлены при
Одинаково направлены при
 3)
3) Имеют противоположные направления при
Имеют противоположные направления при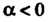 (рис. 3.7). Оче
(рис. 3.7). Оче
Видно, Если
Если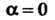 Или
Или
Произведение вектора на число обладает следующими свойствами:
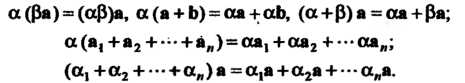
Необходимое и достаточное условие коллинеарности векторов Выражается равенством
Выражается равенством
B = «а.
| < Предыдущая | Следующая > |
|---|