02.11. Некоторые трансцендентные линии
Трансцендентной называется линия, уравнение которой в прямоугольных декартовых координатах не является алгебраическим. Простейшими примерами трансцендентных линий могут служить графики функций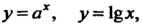
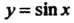И других тригонометрических функций.
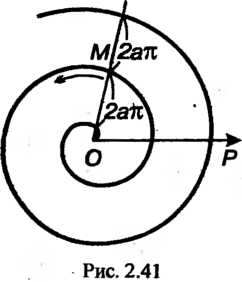
Спираль Архимеда - траектория точки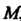
, равномерно движущейся по прямой, которая равномерно вращается вокруг фиксированной точки О (рис. 2.41).
Уравнение спирали Архимеда в полярных координатах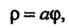 
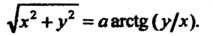
Траектория фиксированной точки окружности, которая без скольжения катится по прямой (см. пример 1.17, уравнения (1.21)).
Рассмотрим траекторию точки,, жестко связанно^ с окружностью, катящейся по прямой, но находящуюся не на самой окружности, а на расстоянии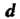
От ее центра При
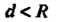Вычерчивающая точка находится
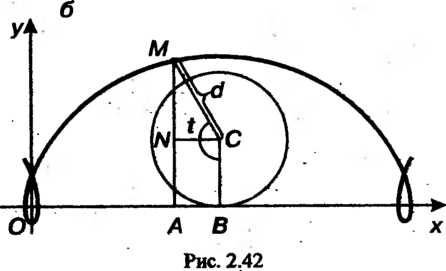
Внутри окружности, ее траекторию называют укороченной циклоидой (рис. 2.42, а). Если
То вычерчивающая точка нахо
Дится вне окружности; ее траекторию называют удлиненной циклоидой
(рис. 2.42, б). Эти линии определяются параметрическими уравнениями
Циклоида —
В декартовых координатах
Алгебраическая спираль - линия, определяемая алгебраическим уравнением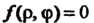 
Относительно полярных координат. К алгебраическим спиралям отно-
Сится спираль Архимеда, так как ее уравнение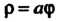
Является алгебраическим
Уравнением первой степени относительно
. Другими. простейшими алгебраическими спиралями являются линии, определяемые уравнениями:
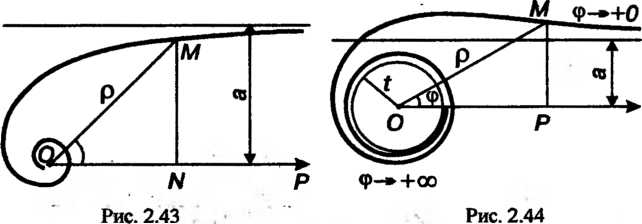
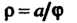(гиперболическая спираль, рис. 2.43);
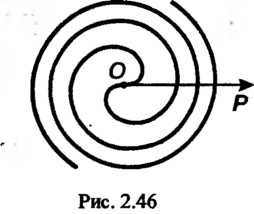
(конховда гиперболической спирали, рис. 2.44);
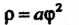(С1шраль Галилея, рис. 2.45);
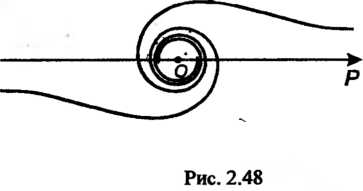
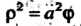(спираль Ферма, рис: 2:46);
(параболическая сйираль, рис. 2.47); \ у
; ¦ > ¦ 4 - -. i * ., ! i}
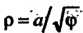‘ ' ' (жезл; рис. 2.48);
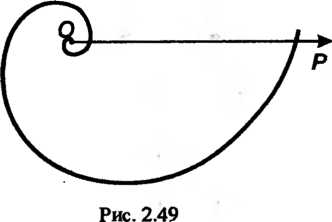
Логарифмической спираль (рис. 2.49) - линия, определяемая уравнением
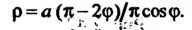
Логарифмическая спираль пересекает полярные радиусы всех своих точек под одним и тем же углом. На этом свойстве основано ее применение в технике. Так, в различных режущих инструментах и машинах вращающиеся ножи имеют профиль, очерченный по дуге логарифмической спирали. В силу этого угол резания остается постоянным. Логарифмическая спираль применяется в теории механизмов при проектировании зубчатых колес с переменным передаточным числом (т. е. отношением их угловых скоростей). В природе некоторые раковины очерчены по логарифмической спирали (рис. 2.50).
Логарифмическая спираль впервые упоминается в письме Декарта к Мерсенну от 12 сентября 1638 г. (опубликовано в 1657 г.). Независимо от Декарта логарифмическая спираль была открыта Торричелли, который выполнил ее спрямление и квадратуру. Название «логарифмическая спираль» для данной линии предложил Лопиталь, автор первого печатного учебника по дифференциальному исчислению.
Квадратриса. Дан отрезок
Длины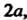
Середина которого находится в точке
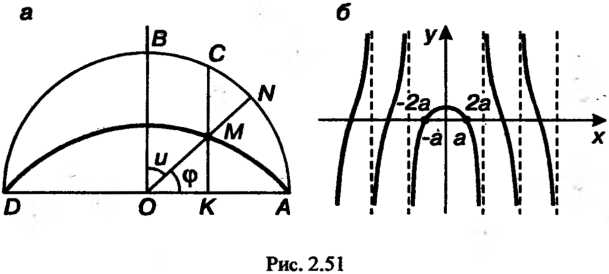
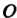(рис. 2.51, в). Отрезок
Равномерно вращается вокруг точки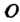
С угловой скоростью
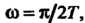А прямая
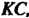Перпендикулярная
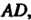Одновременно начинает
Равномерно двигаться от точней
К точке _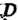
Сач скоростью
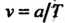, оставаясь па
Раллельной исходному щтравленщо. Точка Ы пересечения вращающегося отрезка и движущейся прямой^писывает линию, к^рую казывают квадратрисой.
Уравнение квадотрисы в декартовых координатах \:
В полярных координатах
Линия имеет бесконечное множество точек пересечения с осью ординат, так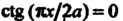 
При
Квадратриса изображена на
Рис. 2.51, б, а на рис. 2.51, а указана та часть линии, которая соответствует значениям аргумента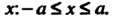
Название линии дал Лейбниц.
Квадратрису впервые открыл Гиппий из Эллиды (древнегреческий софист, I живший в V в. до н. э.) в поисках решения задачи о трисекции угла. К задаче о ' квадратуре круга эту линию применил древнегреческий геометр Динострат IV в. до н. э. В связи с этим линию называют квадратрисой Динострата.
Трактриса - линия, у которой длина касательной является постоянной величиной. Под длиной касательной понимают длину отрезка МТ, касательной между точкой касания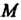
И точкой
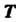Пересечения с осью
(рис. 2.52). Трактриса имеет параметрические уравнения
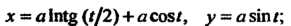
Ее уравнение в прямоугольных декартовых координатах
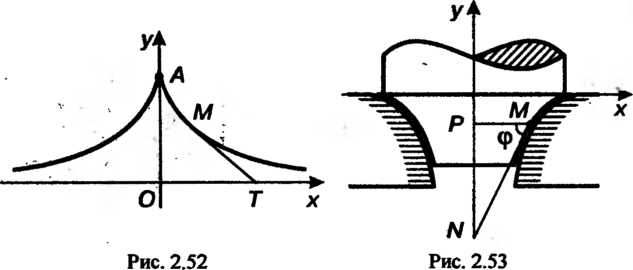
Трактриса применяется в одной из частей механизма карусельного токарного станка (рис. 2.53). Линия вертикального профиля антифрикционной пяты этого механизма обладает тем свойством, что длина ее касательной постоянна.
Трактриса сыграла выдающуюся роль в истории математики в связи с открытием Н. И. Лобачевским новой геометрии и последующим развитием учения о неевклидовых геометриях. Геометрия Лобачевского реализуется на псевдосфере, полученной вращением трактрисы вокруг ее асимптоты.
Трактриса была открыта в XVII в. Ее название происходит от латинского слова traclo - тащу, влеку.
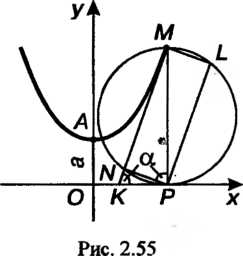
Цепная линия - кривая, форму которой принимает под действием силы тяжести нить с закрепленными концами (рис. 2.54). В прямоугольных декартовых координатах цепная линия имеет уравнение
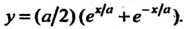
Длина дуги цепной линии от ее вершины до заданной точки равна проекции ординаты этой точки на касательную, проведенную в этой точке (рис. 2.55,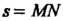
). Проекция ординаты произвольной точки цепной линии
На нормаль в этой точке является величиной постоянной, равной параметру а цепной линии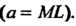
Свойства цепной линии применяются в строительстве и технике. Они используются в расчетах, связанных с провисанием нитей-проводов, тросов и т. д. В строительной технике применяется также линия свода, определяемая уравнением
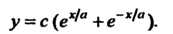
Вопрос о форме линии провисания впервые рассмотрел Галилей (1638). Он полагал, что линия провисания является параболой. Против этого позже возражал Гюйгенс. Окончательное теоретическое решения вопроса о форме линии провисания дали Лейбниц, Гюйгенс, Я. Бернулли.
Понятие вектора возникло как математическая абстракция объектов, характеризующихся величиной и направлением, например, таких как перемещение, скорость и т. п. Термин «вектор» ввел У. Гамильтон (около 1845 г.), обозначения:
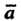- Ж. Арган(1806),
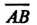- А Мебиус,
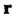- Коши (1853),
- О. Хевисайд (1891)
| < Предыдущая | Следующая > |
|---|
