02.10. Некоторые алгебраические линии высших порядков
Декартов лист - линия, определяемая в прямоугольной декартовой системе координат алгебраическим уравнением


В полярных координатах уравнение принимает вид
Декартов лист можно задать и параметрическими уравнениями
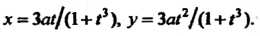
Линия эта изображена на рис. 2.18.
Циссоида. Рассмотрим окружность с диаметром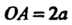 И касательную к ней
И касательную к ней
В точке (рис. 2.19). Из точки
(рис. 2.19). Из точки Проведем луч
Проведем луч , точку его пересечения с окружностью обозначим буквой
, точку его пересечения с окружностью обозначим буквой На этом луче отложим отрезок
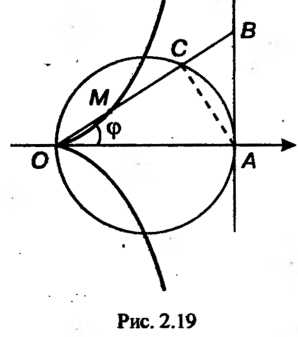
На этом луче отложим отрезок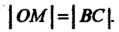

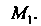
Проведя другой луч и выполнив аналогичное построение, получим точку Таким способом можно построить сколько угодно точек. Множество точек  Называют циссоидой. Построив достаточное число указанных точек и
Называют циссоидой. Построив достаточное число указанных точек и
Соединив их плавной линией, получим циссоиду (см. рис. 2.19).
Уравнение циссоиды в декартовых прямоугольных координатах имеет вид
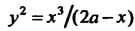 »
»
В полярных координатах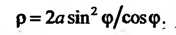 Параметрические уравнения циссоиды
Параметрические уравнения циссоиды

Или

Где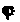 - полярный угол.
- полярный угол.
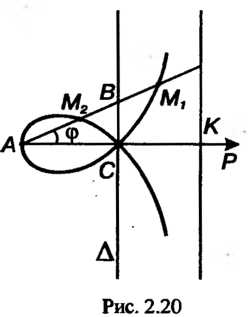
Строфоида. Рассмотрим точку И прямую
И прямую , не проходящую через данную точку (рис. 2.20). Обозначим буквой
, не проходящую через данную точку (рис. 2.20). Обозначим буквой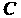 Точку пересечения перпендикуляра к прямой
Точку пересечения перпендикуляра к прямой , проведенной в точке
, проведенной в точке , а длину отрезка
, а длину отрезка Т. е.
Т. е.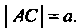 Вокруг точки А вращается луч, на котором откладываются отрезки
Вокруг точки А вращается луч, на котором откладываются отрезки И
И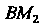 От точки В пересечения с данной прямой так, что
От точки В пересечения с данной прямой так, что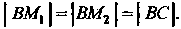 Каждому положению луча соответствует пара точек
Каждому положению луча соответствует пара точек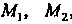 , построенных указанным способом. Множество пар точек
, построенных указанным способом. Множество пар точек Называют строфоидой. Точки
Называют строфоидой. Точки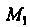 И
И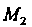 При этом “ называют сопряженными. Построив достаточное число точек и соединив их плавной линией, получим строфоиду (см. рис. 2.20). Название «строфоида» происходит от греческого слова спро<рг| - поворот.
При этом “ называют сопряженными. Построив достаточное число точек и соединив их плавной линией, получим строфоиду (см. рис. 2.20). Название «строфоида» происходит от греческого слова спро<рг| - поворот.
Уравнение строфоиды в полярных координатах
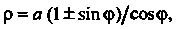
В декартовых координатах

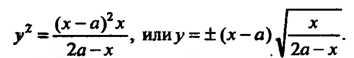
Параметрические уравнения строфоиды
Версьер». Рассмотрим окружность с диаметром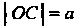 И отрезок
И отрезок По
По
Строенный так, тго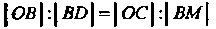 (рис. 2.21). Множество точек
(рис. 2.21). Множество точек
Называют версьерой.
В прямоугольных декартовых координатах уравнение версьеры имеет вид
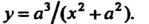
Параметрические уравнения версьеры
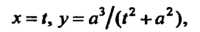

Где роль параметра играет первая координата
Рассматриваемую линию называют так же «локоном Аньези» в честь первой в Европе женщины, получившей известность благодаря заслугам на поприще математики.
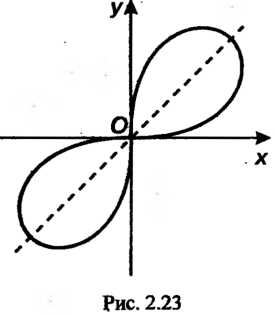
Лемниската Бернулли — множество всех точек плоскости, для каждой из которых произведение расстояний до двух данных точек той же плоскости есть посто
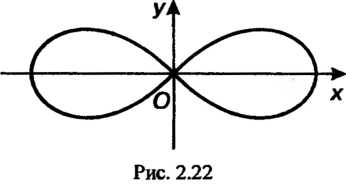
Янная величина, равная квадрату половины расстояния между данными точками.
В декартовых прямоугольных координатах лемниската Бернулли (рис. 2.22) имеет уравнение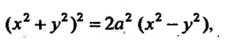
В полярных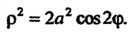
При другом выборе системы координат (рис. 2.23) эта линия определяется соответственно уравнениями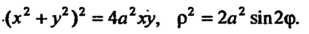
Название линии происходит от греческого слова - повязка, бант.
- повязка, бант.
Линия названа по имени ученого, открывшего ее. Уравнение лемнискаты впервые
Встречается в статье Я. Бернулли, опубликованной в 1694 г. в журнале «Acta eru-ditonim» («Труды ученных»).
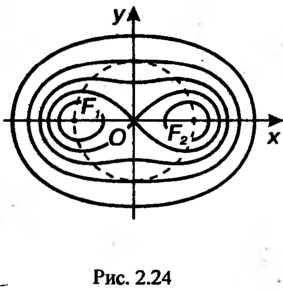
Овал Кассини — множество всех точек плоскости, для каждой из которых произведение расстояний до двух данных точек той же плоскости есть постоянная величина.
Уравнение овала Кассини в декартовых координатах
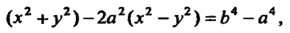
В полярных

Ввд овала Кассини зависит от соотношения между постоянными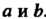 . В случае
. В случае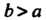 Овал имеет форму замкнутой линии, симметричной относительно осей координат (рис. 2.24). При
Овал имеет форму замкнутой линии, симметричной относительно осей координат (рис. 2.24). При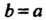 Получаем лемнискату Бернулли. В случае
Получаем лемнискату Бернулли. В случае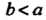
Овал состоит из двух замкнутых линий.
Овалы Кассини названы в честь французского ученного, впервые рассмотревшего их. Жан Доминик Кассини (1625 — 1712) открыл эти линии при попытке определить орбиту земли.
Конхоида. В плоскости фиксируем прямую и точку, отстоящую от этой прямой на расстоянии (рис. 2.25, а). Проведем луч
(рис. 2.25, а). Проведем луч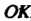 , пересекающий
, пересекающий
Прямую В точке
В точке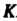 . На луче от точки
. На луче от точки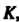 По обе стороны от нее, отложены два отрезка
По обе стороны от нее, отложены два отрезка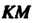 И
И Таких, что
Таких, что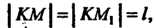 Где
Где - заданное число. Вращая
- заданное число. Вращая
Луч вокруг точки (от 0 до 180° ) и проводя аналогичные построения (при одном и том же значении
(от 0 до 180° ) и проводя аналогичные построения (при одном и том же значении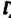 ), получим линию, описываемую точками
), получим линию, описываемую точками И
И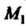 , которую называют конхоидой. Точку
, которую называют конхоидой. Точку При этом называют полюсом конхоиды, а прямую
При этом называют полюсом конхоиды, а прямую
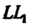 - ее базисом. Линия эта состоит из двух ветвей: одну ветвь описывает точка
- ее базисом. Линия эта состоит из двух ветвей: одну ветвь описывает точка 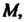 Другую - точка
Другую - точка

Уравнение конхоиды в полярных координатах
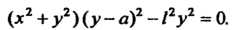
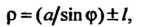
Знак плюс — для верхней ветви, минус — для нижней. Форма конхоиды зависит от соотношения между параметрами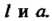 При
При Линия имеет вид,
Линия имеет вид,
Изображенный на рис. 2.25, б, в.
В прямоугольных декартовых координатах конхоида имеет уравнение
Линию эту называют конхоидой Никомеда, по имени древнегреческого геометра, впервые открывшего ее.
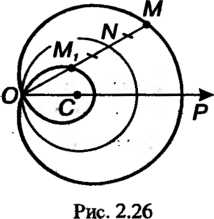
Улитка Паскаля. Рассмотрим окружность радиуса С центром в точке
С центром в точке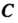 (рис. 2.26). Выберем на данной окружности точку
(рис. 2.26). Выберем на данной окружности точку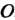 . Представим себе, что вокруг точки
. Представим себе, что вокруг точки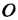 Вращается луч
Вращается луч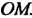 В каждом его положении от точки
В каждом его положении от точки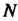 Пересечения луча и окружности откладываем отрезок
Пересечения луча и окружности откладываем отрезок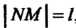 , где
, где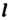 - заданное положительное
- заданное положительное
Число. При повороте луча от.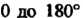 Получим множество точек
Получим множество точек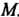 . При даль
. При даль
Нейшем повороте луча от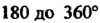 , откладывая отрезок длины
, откладывая отрезок длины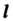 По направле
По направле
Нию луча, мы фактически будем откладывать его в сторону, противоположную

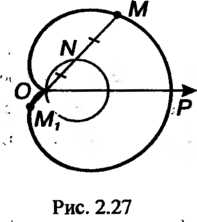
Прежней, т. е.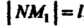 , и получим точки
, и получим точки . Множество точек
. Множество точек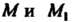 Назы
Назы
Вают улиткой Паскаля.
Уравнения улитки Паскаля:
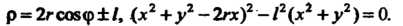
Форма улитки Паскаля зависит отсоотношения между параметрами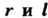
 (рис. 2.26),
(рис. 2.26),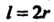 (рис. 2.27),
(рис. 2.27),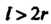 (рис. 2.28).
(рис. 2.28).
Линия названа в честь Этьена Паскаля - французского математика-любителя, отца знаменитого Блеза Паскаля.
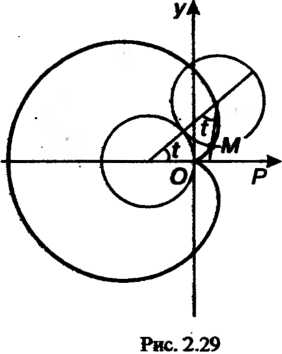
Кярдмодя - линия, описываемая точкой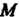 Окружности радиуса г, катящейся по окружности с таким же радиусом (рис. 2.29). Параметрические уравнения кар-диоды
Окружности радиуса г, катящейся по окружности с таким же радиусом (рис. 2.29). Параметрические уравнения кар-диоды
В полярных координатах  в декартовых координатах
в декартовых координатах

Уравнение Также определяет кардиоду в полярной системе коор
Также определяет кардиоду в полярной системе коор
Динат с полюсом в той же точке и противоположно направленной полярной осью.
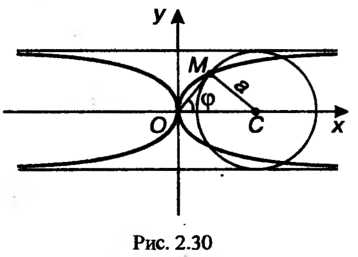
Китая - линия, представляющая собой множество точек касания касательных, проведенных из данной точки к окружности заданного радиуса, центр которой перемещается по фиксированной прямой, проходящей через эту точку (рис. 2.30).
Линия эта напоминает треческую букву к (каппа), откуда и происходит ее название. Параметрические уравнения каппы 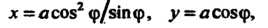
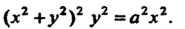
Роза - линия, заданная полярным уравнением Или уравнением
Или уравнением
 Где
Где - положительные числа. Роза целиком расположена в круге
- положительные числа. Роза целиком расположена в круге
Радиуса Так как
Так как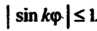 . Роза состоит из конгруэнтных лепестков,
. Роза состоит из конгруэнтных лепестков,
Симметричных относительно наибольших радиусов, каждый из которых равен а. Количество этих лепестков зависит от числа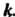 . Если
. Если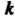 — целое число, то роза состоит из
— целое число, то роза состоит из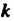 Лепестков при нечетном
Лепестков при нечетном И из
И из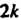 Лепестков при четном
Лепестков при четном (рис. 2.31, а, 6). Если
(рис. 2.31, а, 6). Если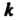 - рациональное число, причем
- рациональное число, причем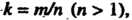 То роза состоит из
То роза состоит из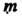
Лепестков в случае, когда - нечетные числа, или из
- нечетные числа, или из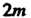 Лепестков, если одно из чисел будет четным. При этом в отличие от предыдущего случая каждый следующий лепесток будет частично покрывать предыдущий (рис. 2.31, в-е).
Лепестков, если одно из чисел будет четным. При этом в отличие от предыдущего случая каждый следующий лепесток будет частично покрывать предыдущий (рис. 2.31, в-е).
Если число Является иррациональным, то роза состоит из бесконечного множества лепестков, частично накладывающихся друг на друга.
Является иррациональным, то роза состоит из бесконечного множества лепестков, частично накладывающихся друг на друга.
Четырехлепестковой розой (см. рис. 2.31, б) называют линию, определяемую полярным уравнением
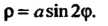
В полярных координатах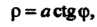 в декартовых координатах
в декартовых координатах
В декартовых координатах линия имеет уравнение 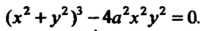
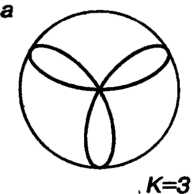

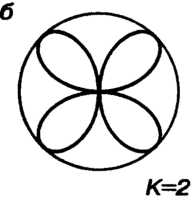
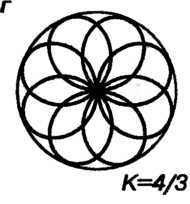
Четырехлепестковая роза образуется множеством оснований перпендикуляров, опущенных из вершины О прямого угла на отрезок постоянной длины, концы которого скользят по двум взаимно перпендикулярным прямым, пересекающимся в точке О.
Трехлепесгковой розой (см. рис. 2.31. а) называют линию, определяемую уравнением
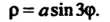
В декартовых координатах линия имеет уравнение
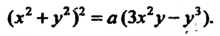
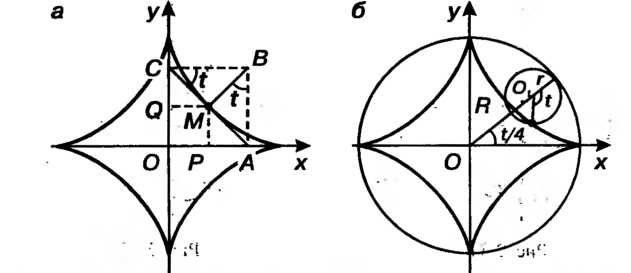
Астроида. Прямоугольник, две стороны которого лежат на двух взаимно перпендикулярных прямых,; деформируется так, что его Диагональ сохраняет постоянную длину р. Множество точек — оснований перпендикуляров, опущенных из вершины прямоугольника наело диагональ, называют астроидой (рис. 2.32, а).
.. 'Астроида 1ше^параметрические уравнения.. ..
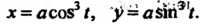
Исключив из этих уравнений параметр t, получим уравнение астроиды в прямоугольных координатах: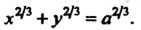
Освобождаясь от дробных показателей, находим

Астроиду можно рассматривать как траекторию точки окружности - радиуса (рис. 2.32, б), катящейся по внутренней стороне другой окружности, радиус
(рис. 2.32, б), катящейся по внутренней стороне другой окружности, радиус Которой в четыре раза больше
Которой в четыре раза больше


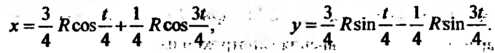
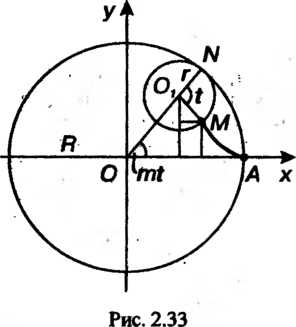
Гипоциклоида - плоская линия, описанная фиксированной точкой окружности радиуса , катящейся без скольжения по другой неподвижной окружности радиуса
, катящейся без скольжения по другой неподвижной окружности радиуса Внутри ее (рис. 2.33, где
Внутри ее (рис. 2.33, где — вычерчивающая точка,
— вычерчивающая точка, - ее исходное положение,
- ее исходное положение,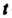 - угол поворота окружности,
- угол поворота окружности, - дуга линии).
- дуга линии).
Параметрические уравнения гипоциклоиды
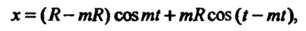
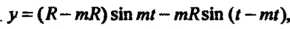
Где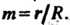 Форма кривой зависит от зна
Форма кривой зависит от зна
Чения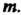 Если
Если
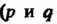 - взаимно
- взаимно
Простые числа), тогда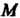 После
После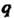 Полных оборотов окружности возвращается в исходное положение и гипоциклоида - замкнутая линия, состоящая из
Полных оборотов окружности возвращается в исходное положение и гипоциклоида - замкнутая линия, состоящая из Ветвей с
Ветвей с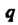 точками возврата при
точками возврата при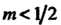 (рис. 2.34);
(рис. 2.34);
При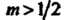 Вместо
Вместо Точек возврата линия
Точек возврата линия
Имеет Других точек (рис. 2.35). При
Других точек (рис. 2.35). При  Линия вырождается в диаметр неподвижной окружности, при
Линия вырождается в диаметр неподвижной окружности, при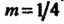 Является астроидой (см. рис. 2.32). При иррациональном т число ветвей бесконечно, точка
Является астроидой (см. рис. 2.32). При иррациональном т число ветвей бесконечно, точка В исходное положение не возвращается. Обобщением гипоциклоиды является гипотрохоида.
В исходное положение не возвращается. Обобщением гипоциклоиды является гипотрохоида.

Гипотрохоида - плоская линия - траектория точки, жестко связанной с окружностью радиуса Катящейся без скольжения по другой неподвижной окружности радиуса
Катящейся без скольжения по другой неподвижной окружности радиуса Внутри ее, причем вычерчивающая точка
Внутри ее, причем вычерчивающая точка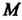 Находится на расстоянии
Находится на расстоянии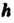 От центра окружности радиуса
От центра окружности радиуса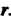 При
При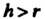 Кривая называется удлиненной гипоциклоидой (рис. 2.36,
Кривая называется удлиненной гипоциклоидой (рис. 2.36, ), при
), при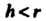 - укороченной (рис. 2.37,
- укороченной (рис. 2.37,  ). Параметрические уравнения гипотрохоиды
). Параметрические уравнения гипотрохоиды
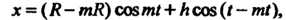

Где При
При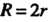 Линия является эллипсом, при
Линия является эллипсом, при - розой (см. рис. 2.31).
- розой (см. рис. 2.31).
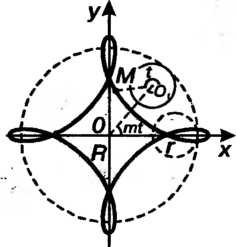
Рис. 2.36
Эпициклоида - плоская линия - траектория фиксированной точки окружности радиуса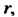 Катящейся без скольжения по другой неподвижной окружности радиуса
Катящейся без скольжения по другой неподвижной окружности радиуса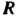 Вне ее (рис. 2.38, где
Вне ее (рис. 2.38, где - вычерчивающая точка,
- вычерчивающая точка,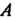 - ее исходное
- ее исходное
Положение,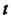 - угол поворота окружности,
- угол поворота окружности,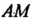 -дуга кривой).
-дуга кривой).
Параметрические уравнения эпициклоиды
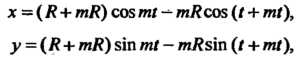
Рис. 2.37

Где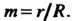 Форма кривой зависит от значения т
Форма кривой зависит от значения т
(рис. 2.39, а;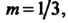 Рис. 2.39, б;
Рис. 2.39, б; ). Если
). Если
 (
(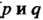 - взаимно простые числа), точка
- взаимно простые числа), точка
После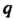 Полных оборотов окружности возвращается в исходное положение и эпициклоида - замкнутая линия, состоящая из
Полных оборотов окружности возвращается в исходное положение и эпициклоида - замкнутая линия, состоящая из Ветвей с
Ветвей с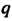 Точками возврата. При
Точками возврата. При Кривая является кардиодой (см. рис. 2.29). При иррациональном
Кривая является кардиодой (см. рис. 2.29). При иррациональном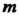 Число ветвей бесконечно, точка
Число ветвей бесконечно, точка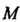 В исходное положение не возвращается. Обобщением эпициклоиды является эпитрохоида.
В исходное положение не возвращается. Обобщением эпициклоиды является эпитрохоида.
Эпитрохоида - плоская кривая - траектория точки, жестко связанной с производящей окружностью радиуса , катящейся без скольжения по другой неподвижной окружности радиуса
, катящейся без скольжения по другой неподвижной окружности радиуса Вне ее, причем вычерчивающая точка
Вне ее, причем вычерчивающая точка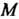 Находится на расстоянии
Находится на расстоянии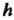 От центра производящей окружности. При,
От центра производящей окружности. При, Линия называется удлиненной эпициклоидой (рис. 2.40, а;
Линия называется удлиненной эпициклоидой (рис. 2.40, а; ), при
), при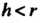 - укороченной эпициклоидой (рис. 2.40, б;
- укороченной эпициклоидой (рис. 2.40, б;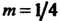 ). Параметрические уравнения эпитрохоиды
). Параметрические уравнения эпитрохоиды
Где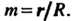 При
При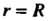 Линия является улиткой Паскаля (см. рис. 2.27,2.28), при
Линия является улиткой Паскаля (см. рис. 2.27,2.28), при
 - розой (см. рис. 2.31).
- розой (см. рис. 2.31).
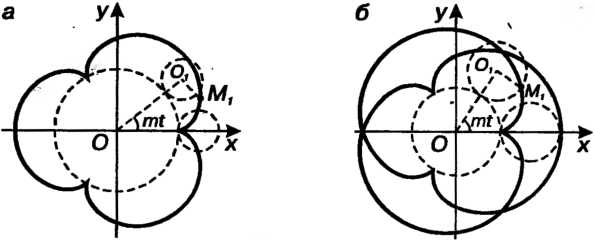
Рис. 2.39
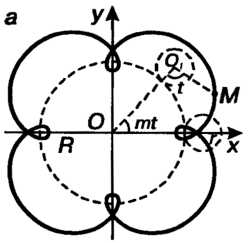
Рис. 2.40

| < Предыдущая | Следующая > |
|---|