02.09. Упрощение общего уравнения второй степени
Общее уравнение второй степени относительно прямоугольных декартовых координат
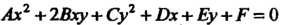 . „ , .. ,(2.51)
. „ , .. ,(2.51)
При повороте координатных осей на угол а, для которого
 (2.52)
(2.52)
Преобразуется в уравнение Являющееся уравне
Являющееся уравне
Нием вида (2.41).
Формулы преобразования координат имеют вид
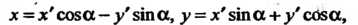 (2.53)
(2.53)
Причем
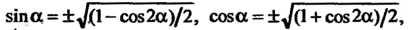 (2.54)
(2.54)
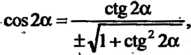 (2.55)
(2.55)
Где^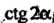 ^ определяемся формул^й»(2.52)У ’ у™ ~%Т. . „ГГ
^ определяемся формул^й»(2.52)У ’ у™ ~%Т. . „ГГ
'Хравийние ф.51) Определяет Диш пустое множество, илйтЪчку, или пару прямы^ (пер^кавдщи^ся, параллельных, совпавйщх), ищи одну из линий (окружность, гшшпс, гипербшту, параболу). Пар/црямых называют распадающейся линией второго порядка. , ‘ • ; > \.
Пример 2.30. Построить линию, дпределяемую уравнением '^ч-

Это частный случай уравнения (2.51), для которого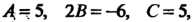
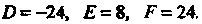 По формуле (2.52) имеем
По формуле (2.52) имеем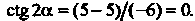 Возь
Возь
Мем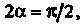 Т. е.
Т. е. Тогда
Тогда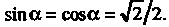 Формулы (2.53) прини
Формулы (2.53) прини
Мают ввд
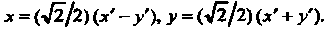
Подставляя эти выражения в исходное уравнение, получаем

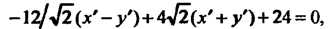
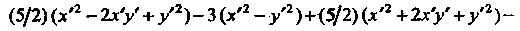
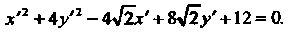
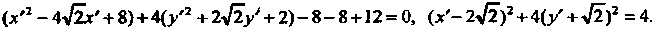
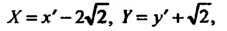
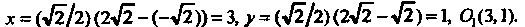
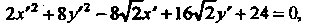

Преобразуем левую часть последнего уравнения, вьщелив в ней полные квадраты: Переходя к новым координатам по формулам
Последнее уравнение записываем так:
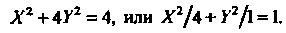 (III)
(III)
Каноническое уравнение (III) определяет эллипс с полуосями По
По
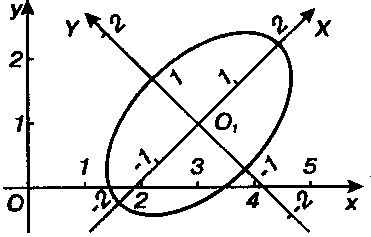
Строим этот эллипс относительно новой системы декартовых прямоугольных координат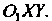 Угол
Угол
Наклона оси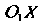 К оси
К оси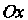 Уже
Уже
Известен , осталось опре
, осталось опре
Делить старые координаты точки 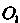 . В системе
. В системе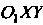 Эта точка
Эта точка
' (центр эллипса) имеет координаты 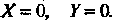 По формулам (II)
По формулам (II)
Имеем
Откуда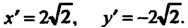 С
С
Помощью формул (I) находим координаты точки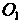 В старой системе координат
В старой системе координат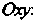
Строим новую систему координат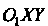 И сам эллипс по его канониче
И сам эллипс по его канониче
Скому уравнению (III) (рис. 2,13).
Пример 2.31. Построить линию, определяемую уравнением
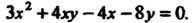
В данном случае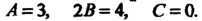 По формуле (2.52) находим
По формуле (2.52) находим
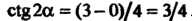 . В формулы (2.53) входят
. В формулы (2.53) входят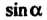 И
И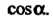 Найдем их значения с помощью формул (2.54) и (2.55), в которых знак можно выбрать по своему усмотрению. Выбрав везде знак плюс, получим
Найдем их значения с помощью формул (2.54) и (2.55), в которых знак можно выбрать по своему усмотрению. Выбрав везде знак плюс, получим
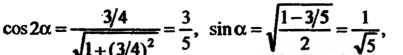
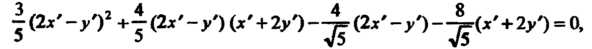
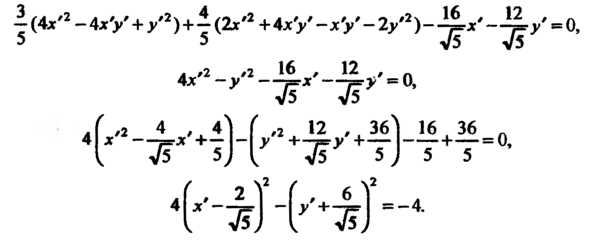
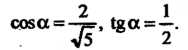
Формулы (2.53) принимают вид
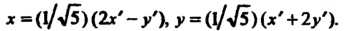 (IV)
(IV)
Подставим эти выражения в исходное уравнение и преобразуем его:
Перейдем к новым координатам по формулам
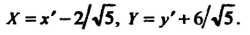 (V)
(V)
Последнее. уравнение в новых координатах примет вид
 Или
Или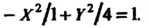
Это каноническое уравнение определяет гиперболу с полуосями причем действительной осью будет ось
причем действительной осью будет ось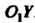 . Построим гиперболу в новой системе координат
. Построим гиперболу в новой системе координат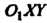 . Найдем сначала старые координаты точки
. Найдем сначала старые координаты точки , в которой находится центр гиперболы. Для этой точки
, в которой находится центр гиперболы. Для этой точки По формулам
По формулам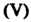 Получаем
Получаем
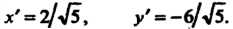 С помощью формул
С помощью формул Находим
Находим
 Через точку
Через точку Проводим ось
Проводим ось , для которой
, для которой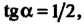 И ось
И ось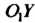 , перпендикулярную оси
, перпендикулярную оси В системе координат
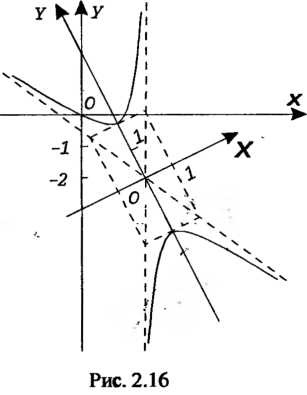
В системе координат Строим гиперболу по ее каноническому уравнению (рис. 2.16).
Строим гиперболу по ее каноническому уравнению (рис. 2.16).
Пример 2.32. Построить линию, определяемую уравнением

Поскольку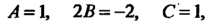 То по формуле (2.52)
То по формуле (2.52)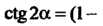
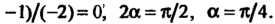 Формулы (2.53) принимают вид
Формулы (2.53) принимают вид
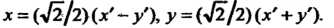 (VI)
(VI)
Подставим эти выражения в исходное уравнение и преобразуем его:
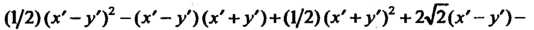

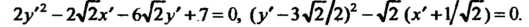
Перейдем к новым координатам по формулам
 (VII)
(VII)
В новых координатах последнее уравнение принимает вид
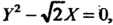 Или
Или

Это уравнениеопределяет параболу. Вершина параболы находится в точке, для которой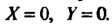 Найдем старые координаты этой точки. По формулам (VII)
Найдем старые координаты этой точки. По формулам (VII)
Находим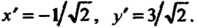 С помощью формул (VI) получаем
С помощью формул (VI) получаем

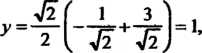
Строим систему координат И параболу по ее каноническому уравнению (рис. 2.17).
И параболу по ее каноническому уравнению (рис. 2.17).
| < Предыдущая | Следующая > |
|---|