02.08. Упрощение уравнения второй степени, не содержащего члена с произведением координат

 

Рассмотрим уравнение второй степени относительно прямоугольных декарто - • вых координат, не содержащее члена с произведением координат ху.

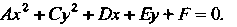(2.41)

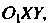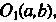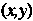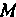Перейдем к новой системе координатПолученной из исходной путем параллельного переноса (см. рис. 1.10) начала в точкуПри котором старые координатыТочкиВыражаются через ее новые координаты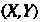Формулами (1.22).

Уравнение (2.41) путем выделения полных квадратов может быть приведено к одному из следующих канонических уравнений:

(2.42)

(2.43)

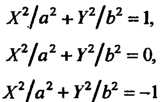(2.44)

В случае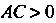(линии эллиптического типа);

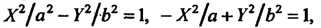(2.45)

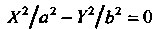(2.46)

В случае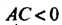(линии гиперболического типа);

Зз

 

2 Зак. I

(2.47)

(2.48)

(2.49)

(2.50)

* в случае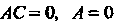(линии параболического типа).

Если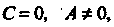То уравнение (2.41) приводится к виду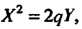Если

ЕФ 0, и к одному из, уравнений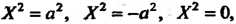Когда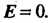

Уравнение (2.42) определяет эллипс, уравнения (2.45) - гиперболы (с дейст-витёяыюй осью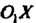Или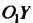), уравнение (2.47) - параболу (с осью),

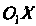Уравнения (2.46) - пару пересекающихся прямых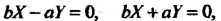

Уравнение (2.48) - пару параллельных прямых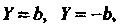Уравнение (2.49) -

Пару совпавших прямых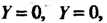Уравнению (2.43) удовлетворяют координа

Ты единственной точки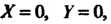Уравнениям (2.44) и (2.50) не удовлетворя

Ют координаты ни одной точки.

Пример 2.28. Построить линию, определяемую уравнением

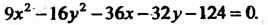
Преобразуем это уравнение:

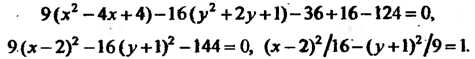
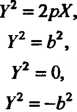
Перейдя к новым координатам по формулам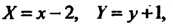Получим

Уравнение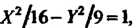Определяющее гиперболу с полуосями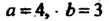

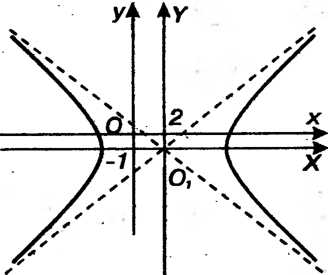
(рис. 2.13). Центр гиперболы находится в точке, для которой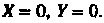Так как

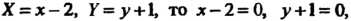Откуда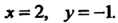Получена точка

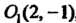, в которой находится начало новой системы координат.

Пример 2.29. Построить линию, определяемую уравнением

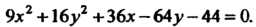
Выделяя полные квадраты в левой части уравнения, получаем

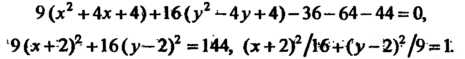(•.» I? ' ' ‘l

Перехрдя к новым координатам по формулам,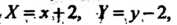Последнему

Уравнению придадим вид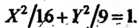. Это уравнение определяет эллщк с полу

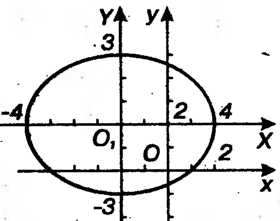
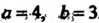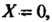
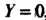Осями(рис. 2.14). Центр эллипса находится у точке, для которой

, или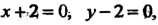Откуда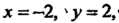Т. е. в точке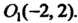

< Предыдущая		Следующая >