02.07. Некоторые другие виды уравнений линий второго порядка
Уравнение Приводится к виду
Приводится к виду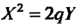 И определяет парабо
И определяет парабо
Лу с осью, параллельной оси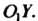
Уравнение Приводится к виду
Приводится к виду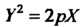 И определяет пара
И определяет пара
Болу с осью, параллельной оси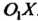
Равносторонняя гипербола имеет уравнение (2.30), а в системе координат, ося-- ми которой являются ее асимптоты, определяется уравнением
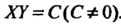 (2.39)
(2.39)
Уравнение

Приводится к виду (2.39) и определяет гиперболу.
Параметрические уравнения эллипса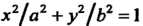 Имеют вид
Имеют вид
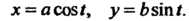
Параметрические уравнения гиперболы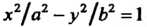 Имеют вид
Имеют вид

А также

Где - гиперболические функции аргумента
- гиперболические функции аргумента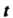 (см. п. 13.11).
(см. п. 13.11).
Параметрические уравнения параболы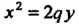 Можно записать так:
Можно записать так:
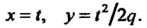
Уравнение
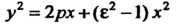 (2.40)
(2.40)
Определяет эллипс при Гиперболу при
Гиперболу при , параболу при
, параболу при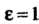 . В слу
. В слу
Чае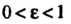 Это уравнение принимает вид
Это уравнение принимает вид
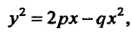
Где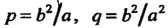 , а в случае
, а в случае Где
Где Имеют те же
Имеют те же
Выражения.
Уравнение (2.40) называют уравнением эллипса, гиперболы, параболы, отнесенных к вершине; начало декартовой прямоугольной системы координат находится в вершине линии - точке пересечения с координатной осью (рис. 2.9).
Эллипс, гиперболу, параболу называют каноническими сечениями. В сечении конуса плоскостью, не проходящей через его вершину (рис. 2.10), получаются эти линии, а именно эллипс (сечение одной полости конуса плоскостью, не перпецди-
Пример 2.25. Построить линию, определяемую уравнением
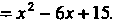 Преобразуя это уравнение, получаем
Преобразуя это уравнение, получаем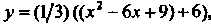
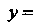
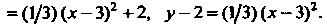
Перейдем к новым координатам по формулам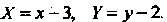 В новых
В новых
Координатах уравнение принимает вид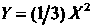 , или
, или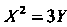 ; оно определяет
; оно определяет
Параболу. Строим системы координат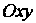 И
И , последнею с началом в точке
, последнею с началом в точке
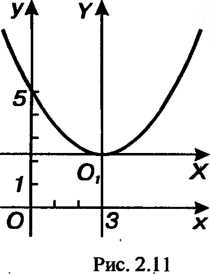
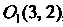 , и саму параболу - в новой системе координат по ее каноническому уравнению (рис. 2.11).
, и саму параболу - в новой системе координат по ее каноническому уравнению (рис. 2.11).
Пример 2.26. Построить линию, определяемую уравнением

Кулярной его оси и не параллельно образующей), парабола (сечение плоскостью, параллельной его образующей), гипербола (речение плоскостью обеих полостей конуса).

Рис. 2.10
Рис. 2.9
Преобразуя данное уравнение:
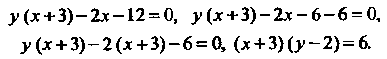
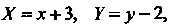
Переходя к новым координатам по формулам получаем
Уравнение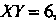 , определяющее гиперболу. Строим линию в системе координат
, определяющее гиперболу. Строим линию в системе координат
 (рис. 2.12), начало которой находится в точке
(рис. 2.12), начало которой находится в точке

Рис. 2.12
Пример 2:27. Какую, линию определяет уравнение ?
?
Преобразуем это уравнение: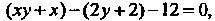
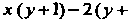


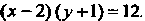
Переходя кновым координатам по формулам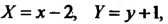 Получаем
Получаем
Уравнение Которое определяет гиперболу.
Которое определяет гиперболу.
| < Предыдущая | Следующая > |
|---|