02.06. Полярное уравнение эллипса, гиперболы, параболы

 

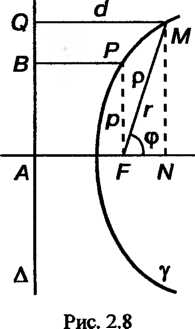
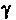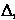Пусть- дуга эллипса, гиперболы или параболы (рис. 2.8). Проведем через фокусПрямую, перпендикулярную директрисе, точку их пересечения обозначим через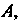Проекцию точкиНа эту прямую - буквой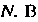Точке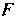Проведем перпендикуляр к прямой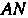(оси линии|, обозначим буквой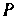Точку ее пересечения с дугой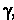, а длину отрезка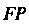- буквой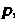, т. е.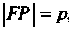, и назовем ее фокаль

Ным параметром линии

Пусть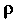И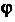— полярныекоординаты точкиВ системе координат с полюсом в точке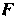И полярной осью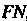, тогда

(2.37)

Уравнение (2.37) называется полярным уравнением эллипса, гиперболы, параболы (это уравнение определяет одну из двух ветвей гиперболы).

Отметим, что для параболы фокальный параметр совпадает с параметром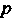, входящим в уравнение (2.33), для эллипса и гиперболы, заданных соответственно уравнениями (2.21) и (2.25), он выражается формулой

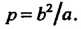(2.38)

Пример 2.23! Какую линию определяет уравнениеВ полярных координатах?

Разделим на 5 числитель и знаменатель правой части уравнения:

Сравнивая полученное уравнение с уравнением

(2.37) и учитывая формулу (2.38), получаем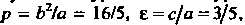Откуда

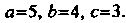Поскольку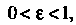То данное уравнение определяет эллипс с по

Луосями

Пример 2.24. Какую линию определяет уравнениеВ по

Лярных координатах?

Разделив числитель и знаменатель правой части на 4, приведем это уравнение к виду (2.37):

Следовательно,Данное уравнение определяет

Гиперболу с полуосями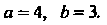

< Предыдущая		Следующая >