02.05. Парабола

 

Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы), лежащих в той же плоскости.

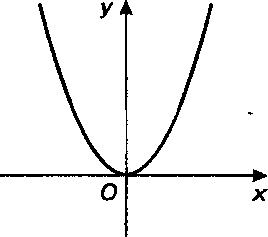
Уравнение параболы, симметричной относительно оси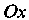И проходящей через начало координат (рис. 2.6), имеет вид

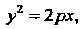(2.33)

Уравнение ее директрисы

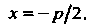(2.34)

Парабола, определяемая уравнением (2.33), имеет фокус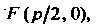Фокаль-

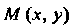
Ный радиус ее точки  вычисляется по формуле

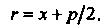- (2.35)

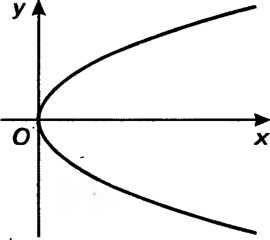
Парабола, симметричная относительно оси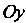И проходящая через начало координат (рис. 2.7), определяется уравнением

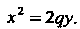(2.36)

Фокус этой параболы находится в точке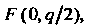Уравнение директрисы имеет вид

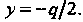Фокальный радиус ее точки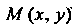Выражается формулой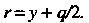

Замечание. Каждое из уравнений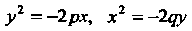Определяет

Параболу.

Пример 2.20. Найти координаты фокуса и уравнение директрисы параболы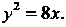Вычислить расстояние точки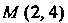До фокуса.

Сравнивая уравнение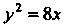С уравнением (2.33), находим, что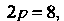Отку

Да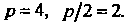В соответствие с формулой (2.34) получаем уравнение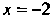

ДиректрИсы параболы, фокус параболы находится в точке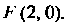Точка

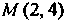Лежит на параболе, так как ее координаты удовлетворяют уравнению

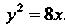. По формуле (2.35) находим фокальный радиус точки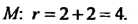

Пример 2.21. Найти координаты фокуса и уравнение директрисы параболы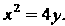Вычислить расстояние точки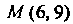До фокуса

Сравнивая уравнение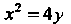С уравнением (2.36), получаем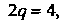Откуда

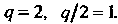Следовательно, фокус параболы находится в точке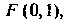Урав

Нение директрисы имеет ввд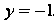, а фокальный радиус т<?чки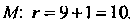

Пример 2.22. Составить уравнение параболы, симметричной относительно оси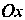И проходящей через точки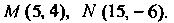

Так как парабола симметрична относительно оси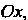То в ее уравнение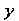Входит только во второй степени. Уравнение этой параболы имеет ввд 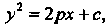Где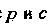— некоторые постоянные. Найдем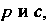Использовав условия задачи. Поскольку точки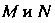Лежат на параболе, то их координаты должны удовлетворять ее уравнению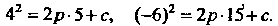Из уравнений 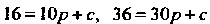Находим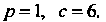

Таким образом, данная парабола определяется уравнением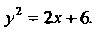

< Предыдущая		Следующая >