02.04. Гипербола

 

Гиперболой называется геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек (фокусов) той же плоскости есть величина постоянная.

Каноническое уравнение гиперболы

(2.25)

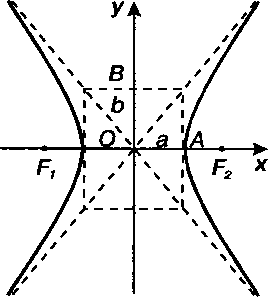
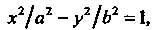
Где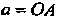- действительная,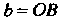- мнимая полуоси (рис. 2.5).

Координаты фокусов гиперболы (2.25):

Т. е.

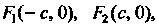Где

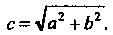(2.26)

Эксцентриситетом гиперболы называется отношение фокусного расстояния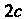К длине действительной оси:

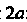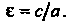(2.27)

Асимптотами гиперболы называют прямые, определяемые уравнениями

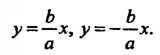
(2.28)

Рис. 2.5

Директрисами гиперболы называются прямые, определяемые уравнениями

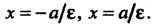(2.29)

Гипербола с равными полуосями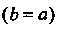Называется равносторонней, ее кано

Ническое уравнение имеет вид

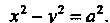(2-30)

Фокальные радиусы точки правой ветви гиперболы вычисляется по формулам

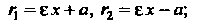(2.31)

Фокальные радиусы точки левой ветви — по формулам

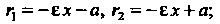(2-32)

Пример 2.17. Какую линию определяет уравнение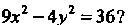 Разделив обе части уравнения на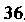, получим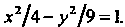Сравнивая это

Уравнение с уравнением (2.25), заключаем, что оно определяет гиперболу с действительной полуосью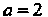И мнимой полуосью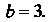

Пример 2.18. Найти полуоси, координаты фокусов и эксцентриситет гиперболы, заданной уравнением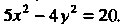Вычислить длины фокальных радиусов точки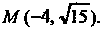

Разделив обе части уравнения на 20, получим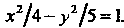Сравнивая это

Уравнение с уравнением (2.25), заключаем, что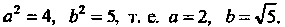

Из формулы (2.26) следует, что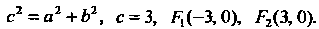По форму

Ле (2.27) находим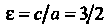. Поскольку точка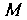Лежит на левой ветви гипер

Болы, то при вычислени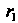иИ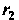Необходимо пользоваться формулами (2.32)

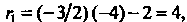
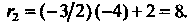Отметим,  что

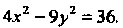
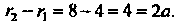
Пример 2.19. Записать уравнения асимптот и директрис гиперболы

Приводя уравнение гиперболы к каноническому виду (2.25), заключаем, что 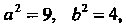Т. е.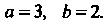В соответствии с (2.28) записываем уравнения

Асимптот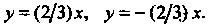По формуле (2.26) находим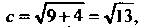

А по формуле (2.27) - эксцентриситет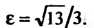Согласно (2.29), получаем

Уравнения директрис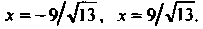

< Предыдущая		Следующая >