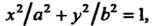02.03. Эллипс
Эллипсом называют геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек (фокусов) той же плоскости есть постоянная величина.
Каноническое уравнение эллипса
Где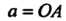 - большая,
- большая, - малая полуоси (рис. 2.4).
- малая полуоси (рис. 2.4).
Координаты фокусов эллипса, определяемого уравнением (2.21):
 Т. е.
Т. е.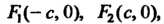 Где
Где
Эксцентриситетом эллипса е называют отношение фокусного расстояния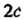 К длине большой оси
К длине большой оси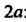
Фокальными радиусами точки Эллипса называют отрезки прямых, соединяющих эту точку с фокусами
Эллипса называют отрезки прямых, соединяющих эту точку с фокусами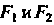 .Их длины
.Их длины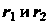 Можно вычислить по формулам
Можно вычислить по формулам
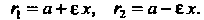 (2.24)
(2.24)
Директрисами эллипса (2.21) называют прямые, определяемые уравнениями
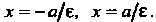
Пример 2.14. Какую линию определяет уравнение ?
?
Разделим это уравнение почленно на
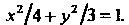 Сравнивая полученное уравнение с уравнением (2.21), заключаем, что оно определяет эллипс с полуосями
Сравнивая полученное уравнение с уравнением (2.21), заключаем, что оно определяет эллипс с полуосями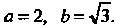
Найдем фокусы этого эллипса. Из формулы (2.22) следует, что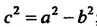 ; поскольку в
; поскольку в
Данном случае
 Следовательно, фокусы эллипса находятся в точках
Следовательно, фокусы эллипса находятся в точках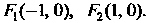
Пример 2.15. В прямоугольной декартовой системе координат построить линию, определяемую уравнением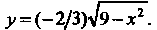
Преобразуем это уравнение, возводя в квадрат обе его части:
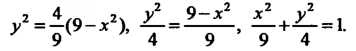
Последнее уравнение определяет эллипс с полуосями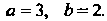 Если решить
Если решить
Это уравнение относительно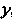 , получим
, получим


В условии задачи дано второе из этих уравнений. Оно определяет не весь эллипс, а только ту его часть, для точек которой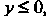 Т. е. половину эллипса, расположенную ниже оси
Т. е. половину эллипса, расположенную ниже оси
Пример 2.16. Записать каноническое уравнение эллипса, проходящего
Через точки
Каноническое уравнение эллипса имеет вид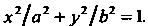 Так как точки
Так как точки И
И
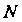 Лежат на эллипсе, то их координаты удовлетворяют уравнению эллипса:
Лежат на эллипсе, то их координаты удовлетворяют уравнению эллипса:
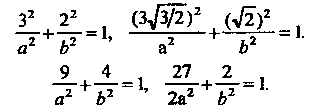
Решая полученную систему уравнений, находим, что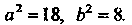
Таким образом, получено каноническое уравнение эллипса
| < Предыдущая | Следующая > |
|---|