02.02. Окружность
Каноническим уравнением окружности радиуса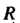 С центром в точке
С центром в точке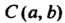 называют уравнение
называют уравнение
Когда центр окружности находится в начале координат, уравнение принимает вид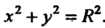
Если уравнение второй степени, не содержащее члена с произведением координат и имеющее равные коэффициенты при И
И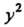 , т. е. уравнение
, т. е. уравнение  Определяет некоторую линию, то эта линия - окружность. Пример 2.12. Найти координаты центра и радиус окружности, определяемой уравнением
Определяет некоторую линию, то эта линия - окружность. Пример 2.12. Найти координаты центра и радиус окружности, определяемой уравнением
Разделив обе части уравнения на 4 и выделив полные квадраты, получим
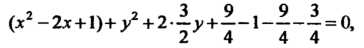
Или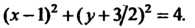
Сравнивая полученное уравнение с уравнением (2.20), заключаем,
Что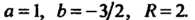
Пример 2.13. Какое множество точек плоскости опредЬляет уравнение  ?
?
Так как это уравнение сводится к уравнению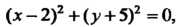 Которому
Которому
Удовлетворяют лишь координаты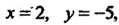 То оно определяет единственную
То оно определяет единственную
Точку
| < Предыдущая | Следующая > |
|---|