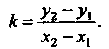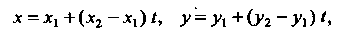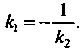02.01. Прямая на плоскости
Прямую линию на плоскости относительно системы декартовых прямоугольных координат можно задать различными способами. Прямая однозначно определяется углом, образуемым ею с осью , и величиной направленного отрезка, отсекаемого на оси
, и величиной направленного отрезка, отсекаемого на оси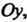 Координатами двух точек и т. п.
Координатами двух точек и т. п.
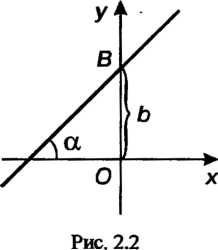
Различные виды уравнения прямой иа плоскости. Прямая, параллельная оси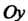 Прямоугольной декартовой системы координат (рис. 2.1), пересекающая ось
Прямоугольной декартовой системы координат (рис. 2.1), пересекающая ось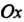 В точке
В точке , имеет уравнение
, имеет уравнение
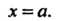 (2.1)
(2.1)
Угловым коэффициентом прямой называют тангенс угла а наклона ее к положительной полуоси Прямоугольной декартовой системы координат
Прямоугольной декартовой системы координат
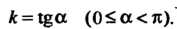
Угловой коэффициент прямой через координаты двух ее различных точек  Определяется формулой
Определяется формулой
Уравнение прямой с угловым коэффициентом имеет вид
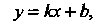 (2.3)
(2.3)
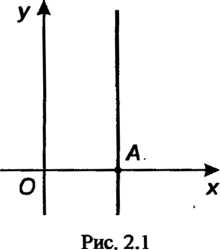
Где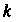 — угловой коэффициент,
— угловой коэффициент, — величина направленного отрезка
— величина направленного отрезка
Отсекаемого на оси (рис. 2.2).
(рис. 2.2).
Уравнение прямой, имеющей угловой коэффициент И проходящей через данную точку
И проходящей через данную точку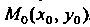 , записывается так:
, записывается так:
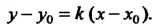 (2.4)
(2.4)
Уравнение прямой проходящей через две данные точки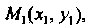
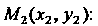
 (2.5)
(2.5)
Параметрические уравнения прямой проходящей через эти точки:
Где t принимает все действительные значения.
Уравнением прямой в отрезках называют уравнение
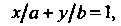 (2.7)
(2.7)
Где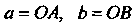 - величины направленных отрезков, отсекаемых соответст
- величины направленных отрезков, отсекаемых соответст
Венно на оси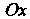 И оси
И оси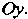
Общим уравнением прямой называют уравнение,
В котором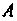 И
И Одновременно в нуль не обращаются, т. е.
Одновременно в нуль не обращаются, т. е.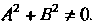
Пример 2.1. Составить параметрические уравнения сторон треугольника, вершины которого находятся в точках
Составим сначала уравнения прямых, на которых лежат стороны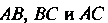 соответственно. Используя уравнение (2.5), получаем
соответственно. Используя уравнение (2.5), получаем
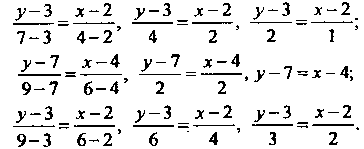
Обозначим буквой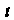 Равные отношения, получим параметрические уравнения этих прямых:
Равные отношения, получим параметрические уравнения этих прямых:
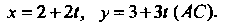
Введя ограничения на изменение параметра *, получим уравнения соответствующих сторон треугольника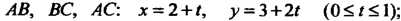
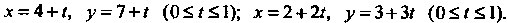
Пример 2.2. Найти величины отрезков, отсекаемых на осях координат прямой, заданной уравнением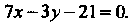
Разделив это уравнение почленно на 21, получим
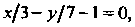 Или
Или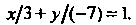
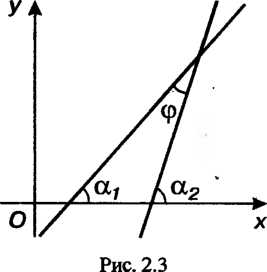
Сравнивая полученное уравнение с уравнением (2.7), заключаем, что Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Тангенс угла между двумя прямыми (рис. 2.3)
Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Тангенс угла между двумя прямыми (рис. 2.3)
 (2.9)
(2.9)
Вычисляется по формуле .
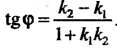
(2.10)
Необходимое и достаточное условие параллельности прямых, заданных уравнениями вида (2.9), выражается равенством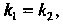 А условие их перпендикулярности - равенством
А условие их перпендикулярности - равенством
Если прямые заданы общими уравнениями  то тангенс угла между ними определяется формулой
то тангенс угла между ними определяется формулой
(2.12)
(2.13)
(2.14)
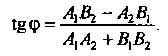
Необходимое и достаточное условие параллельности прямых, заданных уравнениями (2.12) и (2.13), выражается равенством
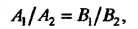 (2.15)
(2.15)
Или
 (2.16)
(2.16)
А условие их перпендикулярности - равенством
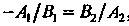 , или
, или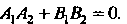 (2.17)
(2.17)
Отметим, что прямые
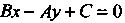 Перпендикулярны в силу
Перпендикулярны в силу
Пример 2.3. Найти угол между прямыми, заданными уравнениями
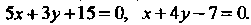
Применяем формулу (2.14). Так как в данном случае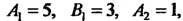
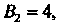 То
То

Замечание. При другой нумерации прямых
 Получаем
Получаем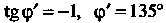 . Очевидно,
. Очевидно,
Пример 2.4. Составить уравнение прямой, проходящей через точку 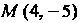 И параллельной прямой
И параллельной прямой Искомое уравнение имеет вид
Искомое уравнение имеет вид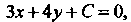 Где
Где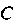 Пока не определено. Вид
Пока не определено. Вид
Уравнения следует из условия (2.1(5) при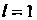 (считаем соответствующие коэффициенты равными). Чтобы найти значение
(считаем соответствующие коэффициенты равными). Чтобы найти значение , необходимо подставить координаты точки М в искомое уравнение (точка.
, необходимо подставить координаты точки М в искомое уравнение (точка.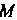 Лежит на прямой, поэтому ее координаты должны удовлетворять уравнению этой прямой). Подставляя координаты
Лежит на прямой, поэтому ее координаты должны удовлетворять уравнению этой прямой). Подставляя координаты
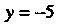 В уравнение
В уравнение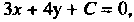 Получаем
Получаем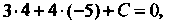 Откуда
Откуда
Таким образом, уравнение прямой имеет вид
Пример 2.5 Составить уравнение прямой, проходящей через точку  И перпендикулярной прямой
И перпендикулярной прямой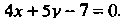 Искомое уравнение имеет вид
Искомое уравнение имеет вид Действительно, для прямых вы
Действительно, для прямых вы
Полнено условие (2.17):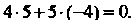 , , Точка
, , Точка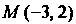 Лежит на прямой
Лежит на прямой
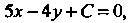 Поэтому ее координаты должны удовлетворять этому уравнению:
Поэтому ее координаты должны удовлетворять этому уравнению:  Отсюда находим, что
Отсюда находим, что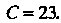 Итак, уравнение прямой прини
Итак, уравнение прямой прини
Мает* вид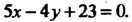
Пример 2.6. Вершины треугольника находятся в точках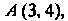
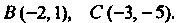 Составить уравнение прямой, на которой лежит высота,
Составить уравнение прямой, на которой лежит высота,
Опущенная из вершины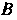 На сторону,
На сторону,
Найдем сначала угловой коэффициент прямой, проходящей через точки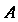 И
И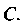 Считая точку
Считая точку Первой, точку
Первой, точку Второй, т. е. полагая
Второй, т. е. полагая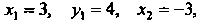
 По формуле (2.2) получаем
По формуле (2.2) получаем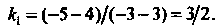 Прямая, на кото
Прямая, на кото
Рой лежит высота, опущенная из точки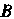 На сторону
На сторону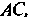 Будет перпендикулярна прямой, проходящей через точки
Будет перпендикулярна прямой, проходящей через точки И
И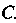 . Угловой коэффициент этой прямой обозначим через
. Угловой коэффициент этой прямой обозначим через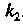 . Используя условие перпендикулярности двух прямых, заданное
. Используя условие перпендикулярности двух прямых, заданное
Формулой (2.11), находим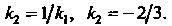
Составим уравнение прямой, проходящей через точку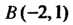 И имеющей
И имеющей
Заданный угловой коэффициент , Подставляя значения
, Подставляя значения
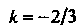 В уравнение (2.4), получаем
В уравнение (2.4), получаем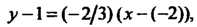
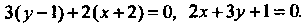
Расстояние от точки до прямой. Уравнения биссектрис углов мзду двумя прямыми. Расстояние от точки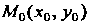 До прямой
До прямой Вычис
Вычис
Ляют по формуле
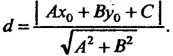 (2.18)
(2.18)
Уравнения биссектрис углов между прямыми
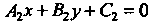 Имеют вид
Имеют вид
 (2.19)
(2.19)
Пример 2.7. Найти расстояние от точки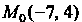 До прямой, заданной
До прямой, заданной
Уравнением *
*
Воспользуемся формулой (2.18). Так как в данном случае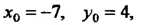
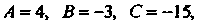 То
То
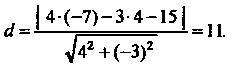
Пример 2.8. Дан треугольник с вершинами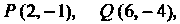
 . Найти длину высоты, опущенной из точки
. Найти длину высоты, опущенной из точки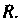 Задача сводится к вычислению расстояния от точки
Задача сводится к вычислению расстояния от точки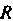 До прямой
До прямой Запишем уравнение этой прямой. На основании уравнения (2.5) имеем
Запишем уравнение этой прямой. На основании уравнения (2.5) имеем Или
Или 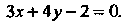 Расстояние точки
Расстояние точки До этой прямой вычислим по формуле (2.18)
До этой прямой вычислим по формуле (2.18)
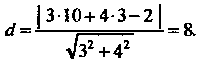
Следовательно, длина высоты равна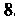
Замечание. Эту задачу можно решить и другими способами. Например, длину искомой высоты можно вычислить, зная площадь треугольника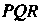 И длину основания
И длину основания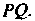 Эта же длина равна расстоянию между двумя точками
Эта же длина равна расстоянию между двумя точками И
И (
(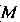 -основание высоты, опущенной из точки
-основание высоты, опущенной из точки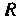 На
На ). В свою очередь координатыточки
). В свою очередь координатыточки  Находятся в результате решения системы уравнений стороны
Находятся в результате решения системы уравнений стороны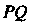 И высоты
И высоты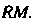
Пример 2.9. Составить уравнения биссектрис углов, образованных прямыми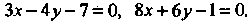
В соответствии с формулой (2.19) получаем 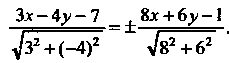
Преобразуя эти уравнения, находим
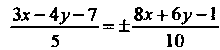

Отсюда получаем уравнения биссектрис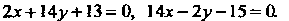
Задачи, относящиеся к прямым. Рассмотрим примеры решения задач, в условиях которых даны уравнения прямых.
Пример 2.10. Даны уравнения двух сторон параллелограмма  И
И И уравнение одной из диагоналей
И уравнение одной из диагоналей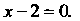 Найти
Найти
Координаты вершин параллелограмма.
Решая систему уравнений
 Находим точку
Находим точку
 — одну из вершин параллелограмма. Две другие вершины найдем как точки пересечения данной диагонали со сторонами, т. е. определим их координаты из систем уравнений
— одну из вершин параллелограмма. Две другие вершины найдем как точки пересечения данной диагонали со сторонами, т. е. определим их координаты из систем уравнений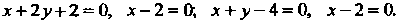 Это будут
Это будут
Точки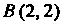 И
И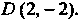 Середина диагонали
Середина диагонали Находится в точке
Находится в точке
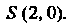 Так как диагонали параллелограмма в точке пересечения делятся пополам, то четвертая вершина
Так как диагонали параллелограмма в точке пересечения делятся пополам, то четвертая вершина Может быть найцена как конец отрезка
Может быть найцена как конец отрезка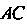 По извест
По извест
Ному концу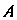 И середине
И середине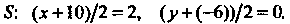 Отсюда получаем
Отсюда получаем
 Т. е. точку
Т. е. точку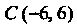 — четвертую вершину параллелограмма
— четвертую вершину параллелограмма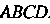
Пример 2.11. Составить уравнение линии, расстояние каждой точки которой до точки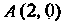 Относится к ее расстоянию до прямой
Относится к ее расстоянию до прямой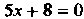 Как
Как
Пусть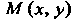 - произвольная точка данной линии,
- произвольная точка данной линии,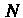 -основание перпен
-основание перпен
Дикуляра, проведенного через точку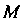 К прямой
К прямой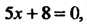 Или
Или Рас
Рас
Стояния точки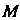 До точки
До точки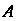 И до прямой
И до прямой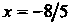 Определяются соответственно
Определяются соответственно
Формулами
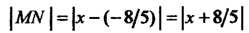 (последнее ра
(последнее ра
Венство следует также из формулы (2.18)). По условию задачи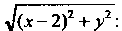
 Откуда
Откуда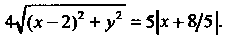 Преобразуем это уравнение:
Преобразуем это уравнение:


Выделим полные квадраты в левой части полученного уравнения:

Последнее уравнение примет вид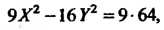 Или
Или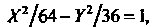 Если
Если
Перейти к новым координатам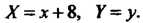
Полученное уравнение определяет гиперболу с полуосями (см.
(см.
Уравнение (2.25)).
| < Предыдущая | Следующая > |
|---|