01.14. Цилиндрические асферические координаты

 

В плоскости П фиксируем точку О и исходящий из нее луч(рис. 1.14). Через точку О проведем прямую, перпендикулярную плоскости П, и укажем на ней положительное направление; полученную ось обозначим. Выберем масштаб для измерения длин. Пусть- произвольная точка пространства, N - ее проекция на плоскость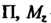- проекция на ось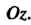Обозначим через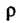И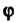Полярные координаты точки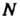В плоскости П относительно полюсаИ полярной оси ОР. Цилиндрическими координатами точки М называются числа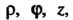Где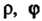-полярные координаты точки,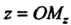- величина направленного отрезкаОсиЗапись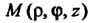Обозначает, что точка М имеет цилиндрические координатыНаименование «цилиндрические координаты»

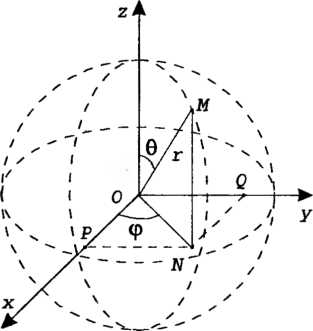
Объясняется тем, что координатная поверхность(т. е. множество точек,

Имеющих одну и ту же первую координату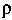) является цилиндром (на рис. 1.14 он изображен штрихами).

Если выбрать систему прямоугольных декартовых координат так, как показано на рис. 1.14, то декартовы координаты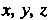Точки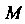Будут связаны с ее цилиндрическими координатами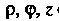Формулами

(1.28)

Сферические координаты вводят следующим образом. Выберем масштаб для измерения длин отрезков, фиксируем плоскость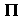С точкой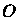И полуосью, ось

, перпендикулярную плоскости(рис. 1.15). Пусть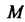— произвольная точка пространства (отличная от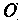),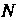— проекция ее на плоскость П, г - расстояние точки Мдо начала координат,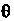—.угол, образуемый отрезкомС осью-угол, на который нужно повернуть ось Ох против часовой стрелки (если смотреть со стороны положительного направления оси Oz), чтобы она совпала с лучом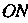; 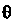Называется широтой,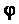— долготой.

Сферическими координатами точки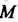Называются три числаОпреде

Ленные выше. Если точкаИмеет сферические координаты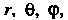То пишут

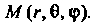
Наименование «сферические координаты» связано с тем, что координатная поверхность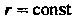(т. е. множество точек, имеющих одну и ту же координату| является сферой (на рис. 1.15 одна из таких сфер изображена штрихами); фиксировав другое значениеПолучим другую сферу.

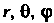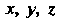Для того чтобы соответствие между точками пространства и тройками сферических координатБыло взаимно однозначным, обычно считают, что изменяются в следующих границах:Если выбрать оси прямоугольной декартовой системы координат так, как указано на рис. 1.15, то декартовы координатыТочки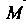Связаны с ее сферическими координатами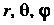Формулами

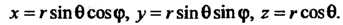(1.29)

Гпава 2

ЛИНИИ НА ПЛОСКОСТИ

Алгебраической линией (кривой)Порядка называют линию, определяемую алгебраическим уравнениемСтепени относительно декартовых координат. Линии первого порядка определяются уравнением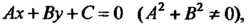 а линии второго порядка - уравнением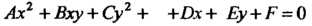

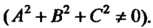
Линии первого порядка - прямые,,Линиям второго порядка относятся окружность, эллипс, гипербола, парабола.

< Предыдущая		Следующая >