01.12. Прямоугольные декартовы координаты в пространстве

 

Прямоугольная декартова система координат в пространстве определяется заданием масштаба (отрезка для измерения длин) и трех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в определенном порядке.

Точка пересечения осей называется началом координат, сами оси - координатными осями, первая из них - осью абсцисс, вторая - осью ординат, третья-осью аппликат. Обозначим начало координат буквой О; координатные оси будем обозначать соответственно через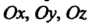(рис. 1.13).

Пусть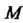- произвольная точка пространства; проведем через нее три плоскости, перпендикулярные координатным осям, и точки пересечения с осями обозначим соответственно через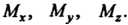Прямоугольными декартовыми координатами точки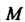Называются числа, определяемые формулами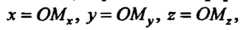

Где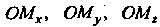— величины

Направленных отрезков,

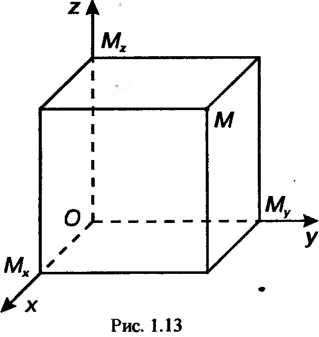
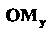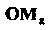,Соответствующих

Координатных осей. Число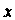Называется первой координатой или абсциссой, число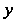- второй координатой или ординатой, число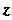-третьей координатой или аппликатой точки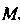

Координатные плоскости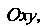

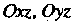Делят все точки пространства, не принадлежащие этим плоскостям, на восемь частей, называемых октантами.

Таблица 1.1

Координата	Октант
I	11	III	IV	V	VI	VII	VIII
X	+	-	-	+	+	-	-	+
У	+	+	-	-	+	+	-	-
Z	+	+	+	+	-	-	-	-

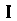
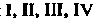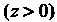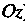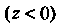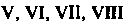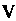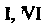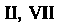Начиная с октанта, в котором все координаты-положительны, пронумеруем октантыВерхнего полупространстваПротив часовой стрелки (для наблюдателя со стороны положительной оси). В нижнем полупространстве Проведем соответствующую нумерацию октантовТак, чтобыНаходился под- под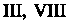- под- под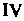. Знаки координат точек в различных октантах приведены в табл. 1.1.

Очевидно, знаки координат однозначно определяют октант пространства.

< Предыдущая		Следующая >