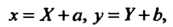01.11. Преобразования декартовых прямоугольных координат на плоскости

 

Одна и та же точка имеет различные координаты в разных системах декартовых координат. Существует связь между координатами точки в разных системах координат.

Параллельный перенос. Пусть даны две системы декартовых прямоугольных координат с общим масштабным отрезком: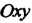(старая) и(новая), соответ

Ствующие оси которых параллельны (рис. 1.10). Положительные полуоси имеют

Одинаковые направления, начало новой системы находится в точке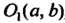, старые

Координаты которой(новые координаты ее равны нулю). Относительно

Таких систем говорят, что одна получена из другой путем параллельного переноса.

Старые координатыТочкиЧерез ее новые координаты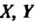И старые координаты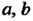Нового началаВыражаются формулами

(1.22)

Откуда

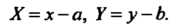(1.23)

Поворот координатных осей. Новая система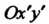Получена путем поворота точки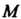Через ее новые координаты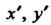Выражаются формулами

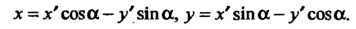(1.24)

Чтобы выразить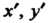ЧерезНеобходимо разрешить систему (1.24) относи-^

Тельно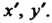Можно сделать проще: считать систему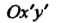Старой, тогда переход

К новой системеСовершается поворотом на угол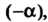Поэтому в формулах

(1.24)  достаточно поменять местам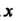и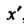И,ИЗаписатьВместо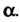

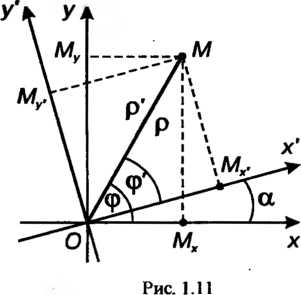
В общем случае, когда даны две системы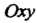И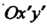(рис. 1.12), вводя про

Межуточную систему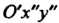И применяя последовательно формулы (1.22) и

(1.24),  получаем

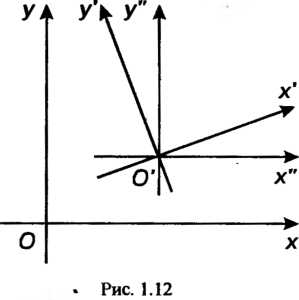
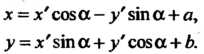
(1.25}

Замечание. Система координат Оху, в которой кратчайший поворот положительной полуоси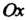До совпадения с положительной полуосью совершается против часовой стрелки, называется правой; если указанный поворот совершается по часовой стрелке, система называется левой.

Формулы (1.25) остаются прежними, если обе системы координат являются левыми. Если одна система правая, другая левая, то в формулах (1.25) изменится знак перед, так как в случае простейшего преобразования координат разноименных систем формулы имеют вид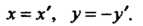

< Предыдущая		Следующая >