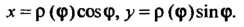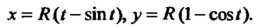01.10. Параметрические уравнения линии
Уравнения вида
 (1.19)
(1.19)
Называются параметрическими уравнениями линии, если при изменении В некотором промежутке формулы (1.19) дают координаты любой точки данной линии и только таких точек.
В некотором промежутке формулы (1.19) дают координаты любой точки данной линии и только таких точек.
Если линия задана уравнением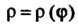 В полярных координатах, то ее пара
В полярных координатах, то ее пара
Метрические уравнения можно записать так:
В уравнениях (1.20) роль параметра играет полярный угол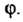
Пример 1.16. Составить параметрические уравнения окружности радиуса с центром в начале координат.
с центром в начале координат.
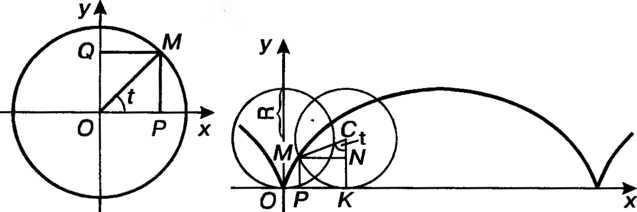
Рис. 1.8 Рис. 1.9
Пусть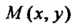 - произвольная точка данной окружности, t - величина угла,
- произвольная точка данной окружности, t - величина угла,
Образуемого отрезком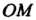 И осью абсцисс,
И осью абсцисс,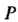 И
И - основания перпендикуляров, опушенных из точки
- основания перпендикуляров, опушенных из точки На координатные оси (рис. 1.8). Так как по определению
На координатные оси (рис. 1.8). Так как по определению  И
И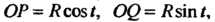 То
То
Следовательно, параметрические уравнения данной окружности имеют вид 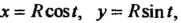 Где
Где
Исключив из этих уравнений параметр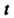 (для чего возведем в квадрат оба равенства и почленно сложим), получим уравнение
(для чего возведем в квадрат оба равенства и почленно сложим), получим уравнение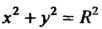 (см. уравнение (1-17)).
(см. уравнение (1-17)).
Пример 1.17. Составить параметрические уравнения циклоиды. Циклоидой называют линию, являющуюся траекторией фиксированной точки окружности радиуса , катящейся по прямой.
, катящейся по прямой.

Указанную прямую примем за ось декартовой прямоугольной системы координат (рис. 1.9). Предположим, что фиксированная точка при начальном положении окружности находилась в начале координат, а после того как окружность повернулась на угол , заняла положение.
, заняла положение.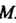 .
.
Поскольку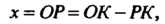
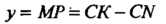 И
И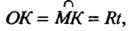
 То
То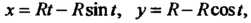 Или
Или
Уравнения (1.21) называются параметрическими уравнениями циклоиды.
| < Предыдущая | Следующая > |
|---|