01.09. Уравнение линии в полярных координатах
Уравнение линии на плоскости в полярных координатах в общем виде можно записать так: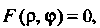
Где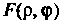 - функция переменных
- функция переменных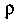 И
И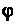
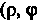 - полярные координаты). Если это
- полярные координаты). Если это
Уравнение разрешимо относительно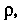 То его можно представить в виде
То его можно представить в виде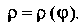
Пример 1.14. Составить уравнение прямой, перпендикулярной полярной оси и отсекающей от нее отрезок, длина которого равна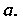
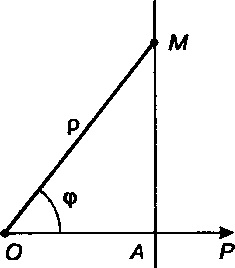
Обозначим буквой А точку пересечения данной прямой с полярной осью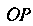 (рис. 1.6). Пусть
(рис. 1.6). Пусть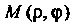 - произвольная точка данной прямой. Из прямоуголь
- произвольная точка данной прямой. Из прямоуголь
Ного треугольника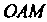 Находим, что
Находим, что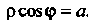 . Полученное уравнение является
. Полученное уравнение является
Искомым; ему удовлетворяют координаты любой точки данной прямой и не удовлетворяют координаты ни одной точки, не принадлежащей этой прямой.

Пример 1.15. Составить уравнение окружности радиуса а, касающейся полярной оси в полюсе, центр которой расположен выше полярной оси (рис. 1.7).
Пусть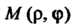 — произвольная точка окружности,
— произвольная точка окружности, — диаметр окружности,
— диаметр окружности,
Равный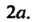 Так как в треугольнике ОАМ угол при вершине М прямой, угол при вершине
Так как в треугольнике ОАМ угол при вершине М прямой, угол при вершине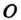 Равен
Равен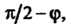 То
То Или
Или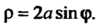 Это искомое
Это искомое
Уравнение данной окружности.
| < Предыдущая | Следующая > |
|---|