01.07. Уравнение линии в декартовых координатах

 

Уравнением линии относительно фиксированной системы координат называют такое, уравнение с двумя переменными, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты ни одной точки, не лежащей на данной линии.

Уравнение линии в декартовых координатах в общем виде записывается так:

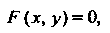
Где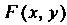— функция переменных х и у.

Пример 1.9. Составить уравнение множества точек, равноудаленных от двух данных точек

Пусть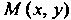- произвольная точка данного геометрического места. По ус

Ловию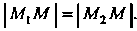По формуле (1.9) получаем

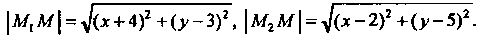
Подставляя эти выражения в равенство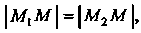Находим уравнение дан

Ного множества точек:

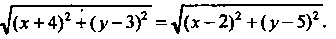
Упростим это уравнение. Возведем в квадрат обе части уравнения и раскроем скобки в подкоренных выражениях:

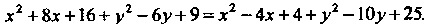
Произведя преобразования, получимЭто уравнение прямой линии.

Пример 1.10. Составить уравнение окружности радиусаС центром в точке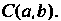

Пусть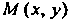— произвольная точка данной окружности. По определению

Окружности (как множества точек, равноудаленных от данной точки) для любой ее

Точки имеем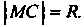Выражая расстояние между точкам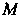иИ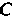По формуле

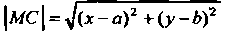И подставляя его в левую часть данного равенства, получим уравнение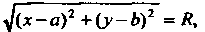Которое можно записать так:

(1.16)

Уравнение (1.16) является уравнением окружности радиуса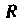С центром в точке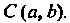

Если точка С совпадает с началом координат, то уравнение (1.16) принимает вид

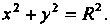(1.17)

Замечание. Если точка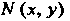Лежит внутри круга радиуса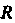С центром в

Начале координат, то ее координаты удовлетворяют неравенству если вне указанного круга, то неравенству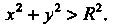

Пример 1.11. Точка Мдвижется так, что в любой момент времени ее расстояние до точки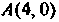Вдвое больше расстояния до точки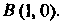Найти уравнение траектории движения точки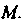

Текущие координаты точки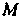В прямоугольной декартовой системе координат обозначим через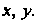По условию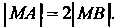Выразим длины отрезков МА и

Через координаты соответствующих точек с помощью формулы (1.9):

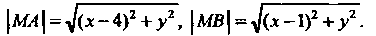
Подставляя эти выражения в равенствоПолучаем уравнение траек

Тории движения точки М: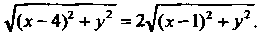Упростим это уравне

Ние, для чего возведем в квадрат обе части и приведем подобные члены

Итак, траекторией движения точки М является окружность радиусаС

Центром в начале координат.

< Предыдущая		Следующая >