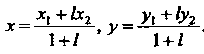01.04. Деление отрезка в данном отношении

 

Отношением, в котором точка. лежащая на прямой, проходящей через точки И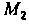, делит отрезок, называют числоОпределяемое формулой (1.3).

Если даны точки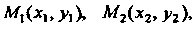То координаты точки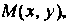Де

Лящей отрезокВ отношении /, определяются формулами

(1.11)

Когда точка М является серединой отрезка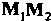, то ее координаты вычис

Ляют по формулам

Пример 1.5. Даны две точки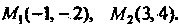На прямо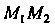йНай

Ти точкуКоторая в три раза ближе к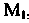, чем к, и находится вне отрезка 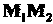. Найти середину этого отрезка.

Искомая точка М делит отрезокВ отношении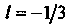. По формулам

(1.11), считая в них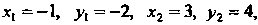Находим

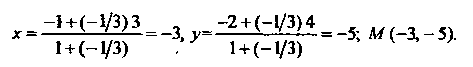
С помощью формул (1.12) находим точку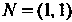— середину отрезка

Пример 1.6. Найти координаты точки пересечения медиан треугольника с вершинами в точках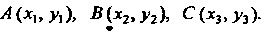

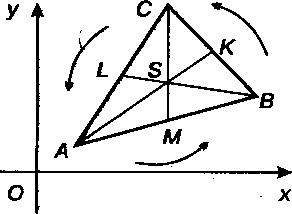
А  б

Рис. 1.5

Пусть- точка пересечения медиан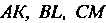Треугольника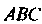

(рис. 1.5, а). Так как точка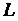- середина отрезка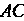Тоона имеет координаты

Отрезок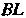Точкой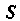Делится в отношении 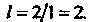Считая точкуПервой, точку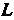Второй, по формулам (1.11) находим

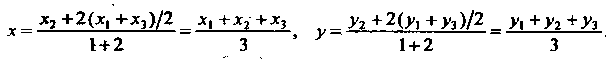
Следовательно, координаты точки пересечения медиан треугольника по координатам его вершин определяются формулами

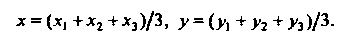
(1.13)

< Предыдущая		Следующая >