06. Признаки сравнения несобственных интегралов от разрывных функций

Общий и предельный признаки сравнения несобственных интегралов от разрывных функций аналогичны таким же признакам для несобственных интегралов по бесконечному промежутку (формулы (4) и (6)). Пусть функции и , неотрицательные на промежутке и интегрируемы на каждом отрезке ,. Тогда, если функции и удовлетворяют на промежутке неравенству: , то имеем: 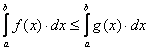и из сходимости интеграла следует сходимость интеграла , а из расходимости интегралаСледует расходимость интеграла . Возможные ситуации сопоставлений интегралов исследуемого и известного такие же, как это представлено в соотношениях . Далее, если существует, отличный от нуля, конечный предел:

(12) ,

То интегралы и ведут себя одинаково: то есть сходятся или расходятся одновременно. В частности, если функции и эквивалентны при , то эти функции одновременно либо интегрируемы, либо неинтегрируемы на промежутке .

В качестве частного признака сравнения несобственных интегралов от разрывных функций используется интеграл с параметром :

(13) ,

Который сходится при И расходится при . В самом деле, 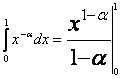, откуда следует, что дробь, стоящая в правой части равенства терпит бесконечный разрыв при и ; если же , то дробь разрыва не имеет и интеграл (13) сходящийся. В более общей форме частный признак сравнения несобственных интегралов от разрывных функций можно представить так:

(13 а, б) или ,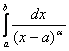

Где, как и раньше, интегралы сходятся при и расходятся при .

Пример 12. Исследовать несобственные интегралы от разрывных функций на сходимость:

А). 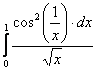; б). ; в). ; г). .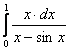

Решения. а). Так как на промежутке имеет место неравенство: 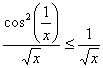, то имеем сопоставление интегралов в виде частного и общего признаков сравнения: .

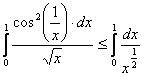Поскольку интеграл в правой части неравенства сходится (формула(13)),то исследуемый интеграл тоже сходится согласно общему признаку сравнения несобственных интегралов.

б). Пусть , а ; тогда имеем сопоставление интегралов: опорного (формула(13а)) и исследуемого в виде предельного признака сравнения (формула (12)): 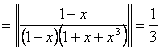; так как опорный интеграл расходится, то расходится и исследуемый интеграл.

в). Используем методику поиска опорного интеграла, описанную для несобственных интегралов первого рода:

1).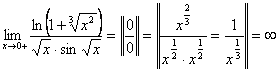, что означает, что подынтегральная функция Имеет одну особенность в точке , где она терпит бесконечный разрыв (при вычислении предела использовалась эквивалентность функций при , а именно: ).

2). в качестве сопоставляемой функции используем 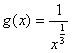, которая эквивалентна функции при ; то есть: , а поскольку интеграл сходящийся (формула(13)), то и исследуемый интеграл тоже сходящийся.

г). Подынтегральная функция Терпит бесконечный разрыв в точке , так как . Исследуя разложение функции в точке , будем иметь: 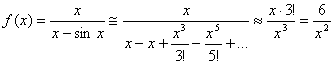; в качестве функции возьмём ; тогда предельный признак сравнения даёт: 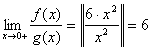, а поскольку расходится, то расходится и исследуемый интеграл.

Упражнения 12. Исследовать интегралы на сходимость:

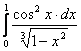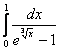а) ; б); в); г).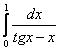

< Предыдущая		Следующая >