07. Абсолютная и условная сходимость несобственных интегралов от разрывных функций

Как и в случае несобственных интегралов по бесконечному промежутку, критерий Коши (формула (3)) для несобственных интегралов от разрывных функций в практических целях мало пригоден (используется иногда для установления расходимости). Тем не менее, определим этот критерий для несобственных интегралов второго рода. Итак, пусть функция F(X) определена на промежутке [A, B), интегрируема на любом отрезке [A, C], С<B, и неограниченна в левой окрестности точки X=B. Тогда для сходимости интеграла необходимо и достаточно, чтобы для любого числа существовало такое число , чтобы при любых и , принадлежащих интервалу , выполнялось соотношение:

(14) .

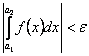Абсолютная и условная сходимость для несобственных интегралов от разрывных функций определяется аналогично тому, как это было сделано для несобственных интегралов по бесконечному промежутку ( см. §5) , а именно: несобственный интеграл от разрывной функций называется абсолютно сходящимся, если сходится интеграл , и условно сходящимся, если интеграл сходится, а интеграл Расходится.

Пример 13. Установить абсолютную сходимость интеграла: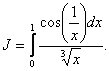

Решение. . Так как последний интеграл сходится, то искомый интеграл J Сходится по общему признаку сравнения, причём сходится абсолютно.

Упражнение 13. Установить абсолютную сходимость интеграла: .

Если абсолютная сходимость несобственного интеграла от разрывной функции места не имеет, то исследовать исходный интеграл на условную сходимость как и в случае с несобственными интегралами по бесконечному промежутку помогают достаточные признаки сходимости Дирихле и Абеля (формулы (7)(11)). В случае несобственных интегралов второго рода упомянутые признаки сходимости определяются так:

15. Признак Дирихле. Интеграл 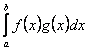сходится, если: 1).функция Непрерывна и имеет ограниченную первообразную на; 2).функция непрерывно дифференцируема и монотонна на , причём.

16. Признак Абеля. Интеграл 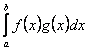сходится, если: 1).функция непрерывна на и интеграл сходится; 2).функция Ограничена, непрерывно дифференцируема и монотонна на , то есть имеет конечный предел:.

Пример 14. Определить характер сходимости интеграла:

.

Решение. Сходимость интеграла устанавливаем с помощью признака Абеля: пусть , тогда , а , и сходимость интеграла: (это несобственный интеграл первого рода от знакопеременной подынтегральной функции, который сходится по признаку Дирихле (см. пример и упражнение №8)), при этом исходный интеграл J сходится по признаку Абеля.

Характер сходимости исходного интеграла J можно установить, исследовав его на абсолютную сходимость, то есть изучив интеграл:

. Так как , то 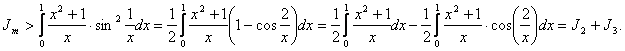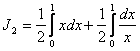Расходится, ,где 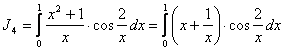; пусть , , ; если x=0+, ; если x =1, t = 2.

Этот интеграл сходится по признаку Дирихле, а интеграл расходится, так как расходится ; итак, исходный интеграл сходится условно.

Упражнение 14. Определить характер сходимости интеграла: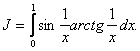

Пример 15. Исследовать сходимость интеграла: .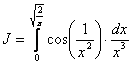

Решение. Исследуемый интеграл имеет одну особенность в точке x=0. Пусть: , , ; если x = 0+, то ; если , .

Тогда: 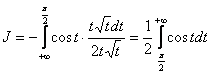и интеграл исходный является расходящимся.

Упражнение 15. Исследовать интеграл на сходимость: .

< Предыдущая		Следующая >