05. Абсолютная и условная сходимость несобственных интегралов по бесконечному промежутку

До сих пор рассматривались интегралы от знакоположительных (знакопостоянных) функций. Теперь пусть подынтегральная функция таких ограничений не имеет, то есть может быть и знакочередующейся функцией.

Если наряду с собственным интегралом по бесконечному промежутку 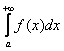Сходится и интеграл по этому же промежутку, то первый интеграл называется Абсолютно сходящимся.

Если интеграл 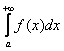Сходится, а интеграл расходится, то первый интеграл называется Условно сходящимся.

Пример 8. Исследовать на абсолютную сходимость интеграл: .

Решение. В начале исследуется данный интеграл вообще на сходимость, для чего проведем интегрированние по частям: пусть тогда , далее . Так как последний интеграл сходится, то по признаку сравнения сходится и интеграл , причем абсолютно. Исходный интеграл при этом является сходящимся (кстати, сходимость этого можно определить быстрее с помощью признака сходимости Дирихле, который будет рассмотрен позже). Чтобы исследовать исходный интеграл на абсолютную сходимость, надо рассмотреть интеграл: . Так как при , то имеем: . Интеграл аналогично исходному интегралу сходится, а интеграл расходится; стало быть, и интеграл является расходящимся. При этом исходный интеграл является условно сходящимся.

Упражнение 8. Установить условную сходимость интеграла: .

Пример 9. Исследовать на абсолютную сходимость интеграл: .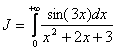

Решение:

; стало быть, интеграл сходится абсолютно.

Упражнение 9. Установить абсолютную сходимость интеграла: .

Установить условную сходимость при отсутствии абсолютной сходимости в ряде случаев позволяет так называемый Признак сходимости Дирихле, в котором исследуется структура подынтегральной функции, если ее можно представить в виде произведения двух функций, а именно: , где интегрируема и ограничена, то есть:

(7) ;

А функция при непрерывно дифференцируема и монотонна, причем:

(8) .

При выполнении условий, налагаемых на функции и интеграл

(9)

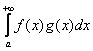
Сходится.

С помощью этого признака условную сходимость интеграла в примере 8 при отсутсвии абсолютной сходимости можно определить следующим образом:

Имеем интеграл , который не является абсолютно сходящимся.

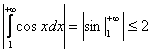Представим подынтегральную функцию этого интеграла в виде произведения двух функций, то есть: , где , а . Функция интегрируема и ограничена на бесконечном промежутке, так как: , а . Поскольку все условия признака Дирихле (Формулы (7) И (8)) выполнены, то исследуемый интеграл сходится условно, ибо абсолютная сходимость этого интеграла места не имеет, что было показано в примере 8.

Пример 10. Исследовать на абсолютную и условную сходимость интеграл:

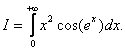
Решение. Сначала сделаем в исследуемом интеграле замену переменной:

Пусть , тогда ; если ; если ; итак, имеем: где является функцией интегрируемой и ограниченной на бесконечном промежутке (формула (7)), а (выполняется формула (8)). Поскольку все условия признака Дирихле (формулы (7) и (8)) выполнены, то исследуемый интеграл сходится. Исследуем интеграл на абсолютную сходимость, для чего рассмотрим интеграл 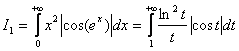. Т. к. при , то . Интеграл сходится по признаку Дирихле, а интеграл расходящийся; стало быть, интеграл тоже расходящийся, при этом исследуемый интеграл сходится условно.

Упражнение 10. Установить условную сходимость интегралов Фронеля:

; .

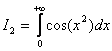Интеграл типа (9) можно исследовать на условную сходимость ещё и с помощью так называемого Признака сходимости Абеля, в котором так же исследуется структура подынтегральной функции, если её можно представить в виде произведения двух функций и , на которые теперь наклкдываются следующие ограничения: интеграл от функции по бесконечному промежутку, то есть:

(10)

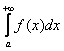
Сходится, а функция при непрерывно дифференциируема, монотонна и непрерывна, а потому имеет конечный предел, то есть:

(11) , .

При выполнении указанных условий ((10) и (11)) интеграл типа (9) сходится.

Пример 11. Установить сходимость интеграла: , используя признак Абеля.

Решение. Исследуемый интеграл представим следующим образом: , где , а . Так как интеграл от функции по бесконечному промежутку сходится (см. пример (8)), а , то все условия признака Абеля выполнены; стало быть, исследуемый интеграл сходящийся. Характер сходимости исходного итеграла (сходится условно или абсолютно) определится после исследования данного интеграла на абсолютную сходимость, для чего надо исследовать интеграл: . Так как , то .

Интеграл сходится по признаку Дирихле, так как 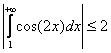, а . Интеграл расходится, что можно установить по предельному признаку сравнения: при ; тогда в кочестве сопоставляемой функции имеем , а , что означает расходимость интеграла . Стало быть, интеграл тоже расходящийся. Теперь ясен и характер сходимости исходного интеграла : он сходится условно.

Упражнение 11. Исследовать характер сходимости интеграла: .

< Предыдущая		Следующая >