04. Признаки сравнения несобственных интегралов по бесконечному промежутку

Вопрос о сходимости несобственного интеграла по бесконечному промежутку эквивалентен вопросу о существовании предельного значения функции 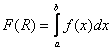при . Для существования предельного значения функции при необходимо и достаточно, чтобы она удовлетворяла следующему условию Коши: для любого можно указать такое А>0, что для любых и , удовлетворяющих соотношению выполняется неравенство:

(3) .

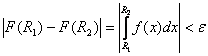В этом утверждении (Критерий Коши) важно то, что сходимость несобственного интеграла по бесконечному промежутку не требует ограниченности подынтегральной функции при (она может быть даже и не определена при ). Критерий Коши мало пригоден для практического применения (используется в ряде случаев для установления расходимости несобственных интегралов по бесконечному промежутку).

Общий признак сравнения. Пусть на полупрямой имеются две неотрицательные функции и , удовлетворяющие неравенству: . Тогда 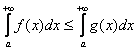и из сходимости интеграла следует сходимость интеграла 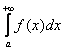, а из расходимости интеграла 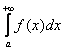следует расходимость интеграла .

Работая с общим признаком сравнения, надо иметь ввиду четыре разные ситуации при сопоставлении исследуемого на сходимость (или расходимость) интеграла и известных (в смысле сходимости) интегралов и . Представим все возможные ситуации при сопоставлении интегралов:

(4.1)

(4.2) сходится;

(4.3) расходится;

(4.4)

Из перечня возможных ситуаций при сопоставлении интегралов следует, что сходится «меньший» от сходящегося интеграла (формула (4.2)) и расходится «больший» от расходящегося интеграла (формула (4.3)); в остальных случаях сопоставления (формулы (4.1) И (4.4)) никакого заключения о поведении исследуемого интеграла сделать нельзя.

Пример 5. Исследовать сходимость несобственных интегралов по бесконечному промежутку с помощью общего признака сравнения:

а). ; б). .

Решения. а). В данном интеграле подынтегральная функция непрерывна на всем промежутке интегрирования; в элементарных функциях исследуемый интеграл «не берется», поэтому сопоставим подынтегральную функцию с другой функцией на всем промежутке интегрирования исходного интеграла, то есть при ; так как в данных условиях , то имеем следующее сопоставление интегралов: . Исследуемый интеграл является «меньшим» по отношению к сходящемуся интегралу, а потому согласию общему признаку сравнения он сходится.

Б). Подынтегральная функция непрерывна и удовлетворяет соотношению при , поэтому имеем следущее сопоставление интегралов: 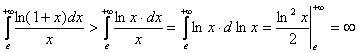; стало быть, «меньший» интеграл расходится, а поэтому «больший» интеграл и подавно будет расходиться согласно общему признаку сравнения (формула (4.3)). Итак, исследуемый интеграл расходящийся.

Упражнение 5. Исследовать сходимость интегралов:

А). 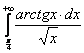; б). .

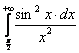В ряде случаев в качестве опорного, реперного, известного интеграла (в смысле сходимости или расходимости) при сопоставлении интегралов по бесконечному промежутку удобно использовать так называемый Частный признак сравнения, то есть интеграл:

(5) ,

Который сходится при и расходится при . Частный признак сравнения несобственных интегралов первого рода есть интеграл с параметром , величина которого обуславливает поведение интеграла в смысле сходимости или расходимости. Так, по определению (1а) Имеем: . При предел конечный и интеграл сходится; при предел бесконечный и интеграл расходится.

Пример 6. Исследовать интегралы на сходимость, используя частный признак сравнения:

а). ; б). .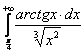

Решения. а). Подынтегральная функция на всем промежутке интегрирования непрерывна и меньше функции . Имеем следующее сопоставление интегралов исследуемого и опорного в виде частного и общего признаков сравнения: . Так как опорный интеграл сходится (формула (5)), то сходится и исследуемый интеграл (формула (4.2)).

Б). Так как подынтегральная функция исследуемого интеграла во всем промежутке интегрирования непрерывна и больше функции , то имеем сопоставление интегралов в виде частного и общего признаков сравнения: 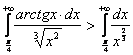. Интеграл в правой части неравенства расходится (формула (5)); стало быть, исследуемый интеграл тоже расходится (формула (4.3)).

Упражнение 6. Исследовать интегралы на сходимость:

А). ; б). .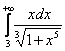

В ряде случаев удобно пользоваться при сопоставлении интегралов так называемым Предельным признаком сравнения, который состоит в том, что рассматривается предел отношения положительных подынтегральных функций сопоставляемых интегралов: опорного 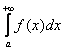и исследуемого при . Если этот предел существует и конечен, то есть:

(6) , ,

То оба интеграла ведут себя одинаково: оба сходятся или оба расходятся. В частности, если функции И Эквивалентны при , то эти функции одновременно либо интегрируемы, либо неинтегрируемые на промежутке .

Пример 7. Исследовать интегралы на сходимость:

а). ; б). .

Решения. а). В качестве опорного интеграла возьмем сходящийся интеграл: . Тогда ; стало быть, исходный интеграл сходится.

б). В качестве опорного интеграла возьмем расходящийся интеграл: . Тогда 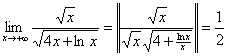; стало быть, исследуемый интеграл расходится.

Основная трудность при определении сходимости или расходимости исследуемого интеграла типа 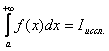с помощью признаков сравнения состоит в выборе опорного интеграла. В ряде случаев можно реализовать следующую методику. 1). Исследуем подынтегральную функцию исходного интеграла; если особенностей у исходного интеграла больше, чем одна, то разбиваем промежуток интегрирования так, чтобы на каждом участке интегрирования было по одной особенности. 2). Пытаемся упростить выражение подынтегральной функции с помощью эквивалентных преобразований при стремлении переменной к особой точке; полученное выражение можно принять за функцию и исследовать интеграл . 3). Зная поведение интеграла , реализуем общий или предельный признаки сравнения.

Пример 7а. Исследовать интегралы на сходимость или расходимость:

1). ; 2). .

Решения. 1). Пусть ; при Имеем: ; за функцию можно принять ; тогда имеем реализацию предельного признака сравнения в виде: ; так как расходится, то расходится и исследуемый интеграл.

2). Подынтегральная функция непрерывна при , так как ; в качестве функции Можно взять ; тогда предельный признак сравнения дает конечное значение, то есть: , а поскольку интеграл сходится, то сходится и исследуемый интеграл.

Упражнение 7. Исследовать интегралы на сходимость:

А).; б).; в).; г)..

< Предыдущая		Следующая >