02. Определение и вычисление несобственных интегралов от разрывных функций

Если подынтегральная функция имеет бесконечный разрыв в точке и непрерывна в окрестности этой точки, то говорят о Несобственном интеграле от разрывной функции или Второго рода, который определяют опять-таки через предельный переход следующим образом:

(2)

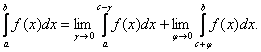
Несобственный интеграл от разрывной функции ,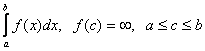

Называется сходящимся, если существуют оба конечных предела в правой части соотношения (2), и – расходящимся, если не существует или равен бесконечности хотя бы один из них. Если разрыв подынтегральной функции находится только в одной из граничных точек промежутка интегрирования (a или b), то есть имеет место лишь один предел в правой части соотношения (2), то говорят о несобственном интеграле второго рода с одной особой точкой.

Пример 3. Вычислить несобственные интегралы от разрывных функций или установить их расходимость:

A). б). в). .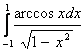

Решения. а). Так как точка разрыва подынтегральной функции находится внутри промежутка интегрирования, то разбиваем его на два участка так, чтобы в каждом было по одной особенности на верхнем или нижнем пределе промежутка интегрирования. Итак, имеем:

;

Стало быть, исследуемый интеграл расходится. Если не учитывать, что подынтегральная функция терпит разрыв внутри промежутка интегрирования, то получим, естественно, неверный результат: .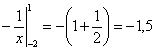

б). Исследуемый интеграл с одной особенностью в точке . Далее имеем: ; стало быть, интеграл сходится и величина его равна .

в). В этом интеграле имеем две особые точки И соответственно на нижнем и верхнем концах промежутка интегрирования. По этой причине исследуемый интеграл разобьём на два интеграла, в каждом из которых будет по одной особенности. Итак, имеем: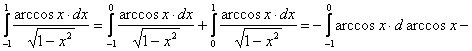

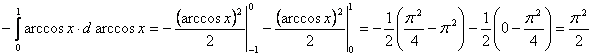; стало быть, исследуемый интеграл сходится и величина его равна .

Упражнение 3. Вычислить интегралы или установить их расходимость:

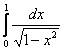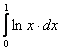А). ; б). ; в). .

Как и в случае несобственных интегралов по бесконечному промежутку для сходящихся несобственных интегралов от разрывных функций также сохраняются основные свойства и формулы определенного интеграла.

Пример 4. Вычислить интегралы:

А). ; б). .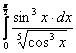

Решения. а). Данный интеграл имеет одну особенность в точке , где подынтегральная функция терпит бесконечный разрыв. Проведём интегрирование по частям: пусть , ; тогда , ; далее имеем: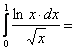

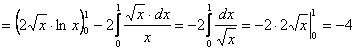, так как

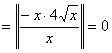. Стало быть, исследуемый интеграл сходится и величина его равна (-4).

б). Данный интеграл имеет одну особенность в точке , подынтегральная функция терпит бесконечный разрыв. Сделаем замену переменной: пусть , ; если , ; если , ; при этом исходный интеграл преобразуется следующим образом :

Стало быть, исследуемый интеграл сходится и величина его равна .

Как и в случае несобственного интеграла по бесконечному промежутку несобственные интегралы от разрывных функций могут превращаться в собственные интегралы при некоторых заменах переменных. Так, например, вычислим интеграл: 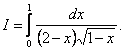Интеграл имеет одну особенность в точке где подынтегральная функция терпит бесконечный разрыв. Сделаем замену переменной: пусть если если При этом заданный несобственный интеграл преобразуется в собственный интеграл следующим образом: (это уже собственный интеграл )

Несобственные интегралы от разрывных функций в некоторых случаях могут превращаться в собственные интегралы при интегрировании по частям. Так, например, вычислим интеграл: Этот интеграл имеет одну особую точку , где подынтегральная функция обращается в бесконечность. Реализуем метод интегрирования по частям: пусть и , тогда и далее имеем: 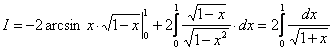(это уже собственный интеграл, который равен ).

Упражнение 4. Вычислить интегралы:

А). 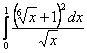; б). ; в). .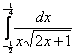

< Предыдущая		Следующая >