1.2. Решение задач

1. Матрица системы имеет вид .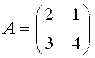

Составим характеристическое уравнение матрицы системы (1.12)

, или

Его корни – характеристические числа матрицы.

При система уравнений (1.10) для определения собственного вектора имеют вид

И сводится к одному уравнению .

Это уравнение имеет бесчисленное множество решений. Найдем одно из них и запишем в виде вектора (1.3).

При получаем систему уравнений (1.10):

.

Это уравнение определяет вектор .

Запишем фундаментальную систему решений: для ; для .

Общее решение системы имеет вид:

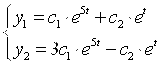
2. Матрица системы Имеет вид .

Составим характеристическое уравнение матрицы системы (1.12):

, или ;

.

Определяем собственные векторы.

При получаем систему уравнений (1.10):

Если , тогда . Получим собственный вектор .

При получаем систему уравнений (1.10):

Таким образом . Приняв , находим , т. е. собственный вектор имеет вид .

Запишем фундаментальную систему решений:

Для :

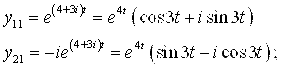
Для :

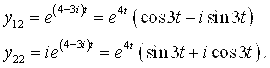
Итак, получаем общее решение:

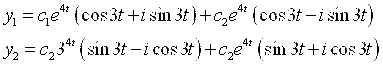
Т. е.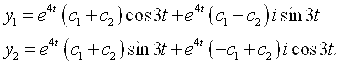

Полагая , получаем

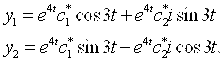
3. Найти фундаментальную систему решений.

Запишем характеристическое уравнение

Корни характеристического уравнения:

Найдем фундаментальную систему решений:

Для получим систему уравнений (1.10):

Для собственный вектор имеет вид

.

Для получили систему уравнений (1.10)

Для собственный вектор имеет вид: .

.

Для получим систему уравнений (1.10)

Для собственный вектор имеет вид .

Фундаментальная система решений представляется в виде:

4. Найти общее решение системы уравнений

Матрица системы : .

Характеристическое уравнение матрицы системы:

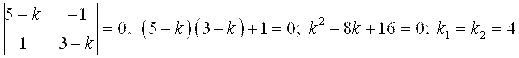
Если – корень кратности , то этому корню соответствует решение

, где – многочлены степени не выше .

Таким образом, двукратному корню соответствует решение .

Дифференцируя и , получим

Значения подставим в исходную систему уравнений. После сокращения на имеем

Приравнивая коэффициенты при и свободные члены, получаем системы уравнений

Отсюда следует, что .

Полагая , находим . Следовательно .

Замечание. Эта система проще решается методом исключения.

< Предыдущая		Следующая >