1.1. Получение фундаментальной системы решений

Характеристическое уравнение (1.12) системы (1.4) является уравнением -ой степени относительно .

Предположим, что характеристическое уравнение имеет различных корней , которые являются характеристическими числами матрицы . Каждому характеристическому числу соответствует свой собственный вектор. Для каждого характеристического числа напишем систему (1.10) и определим собственный вектор .

Тогда система дифференциальных уравнений имеет решений:

1-е решение, соответствующее корню :

2-е решение, соответствующее корню :

;

…………………………………………………

-е решение, соответствующее корню :

.

Мы получили фундаментальную систему решений. Общее решение системы (1.4) таково:

,

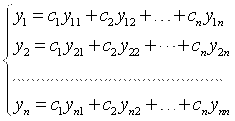Где – произвольные постоянные.

Случаи комплексных и кратных корней рассмотрим на примерах.

< Предыдущая		Следующая >