6.6 Порядки бесконечно малых величин
Бесконечно малая величина ![]() при
при ![]() называется бесконечно
называется бесконечно
Малой ![]() -го порядка малости относительно бесконечно малой величины
-го порядка малости относительно бесконечно малой величины ![]() при
при ![]() ,если существует конечный предел
,если существует конечный предел  не равный нулю.
не равный нулю.
Чаще всего приходится устанавливать порядок малости бесконечно малой ![]() при
при ![]() относительно
относительно ![]() . Задача сводится к тому, чтобы подобрать
. Задача сводится к тому, чтобы подобрать ![]() таким образом, чтобы
таким образом, чтобы ![]() и
и ![]() были одного порядка малости.
были одного порядка малости.
Пример 1. Определить порядок малости функции ![]() относительно
относительно ![]() , т. е. выделить ее “главную часть”.
, т. е. выделить ее “главную часть”.

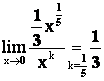
Ответ: Функция ![]() - бесконечно малая порядка
- бесконечно малая порядка ![]() относительно
относительно ![]() , т. е.
, т. е. ![]()
Пример 2. Определить порядок малости функции ![]() Относительно
Относительно ![]() , т. е. выделить ее «главную часть».
, т. е. выделить ее «главную часть».

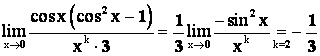
Ответ: Функция ![]() бесконечно малая 2-го порядка малости относительно
бесконечно малая 2-го порядка малости относительно ![]()
![]() .
.
Пример 3. Установить относительный порядок малости при ![]() функций
функций ![]() и
и ![]() .
.

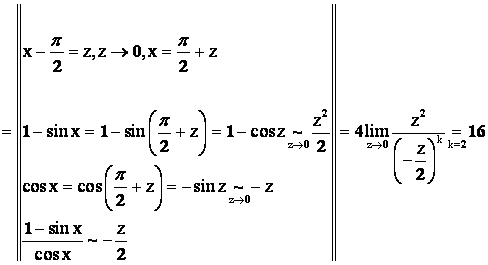 .
.
Ответ: Бесконечно малая функция ![]() 2-го порядка малости относительно бесконечно малой функции
2-го порядка малости относительно бесконечно малой функции ![]() .
.
Пример 4. Убедиться в том, что функция ![]() И
И ![]() при
при ![]() будут бесконечно малыми одного порядка.
будут бесконечно малыми одного порядка.
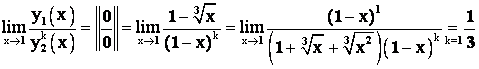 .
.
Ответ: Функции ![]() И
И ![]() - бесконечно малые одного порядка, т. к. предел их отношения при
- бесконечно малые одного порядка, т. к. предел их отношения при ![]() равен
равен ![]() .
.
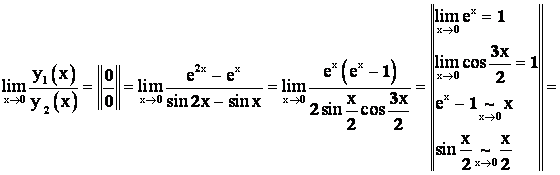
Пример 5. Доказать, что при ![]() Бесконечно малые функции
Бесконечно малые функции ![]() и
и ![]() будут эквивалентными.
будут эквивалентными.
Решение: Составляем предел отношения функций ![]() и
и ![]() , убеждаемся в процессе вычисления, что он равен 1, откуда делаем вывод:
, убеждаемся в процессе вычисления, что он равен 1, откуда делаем вывод:
![]() .
.
 .
.
Что и требовалось доказать: ![]() .
.
Пример 6. Найти относительный порядок малости при ![]() Двух бесконечно малых функций
Двух бесконечно малых функций ![]() и
и ![]() .
.
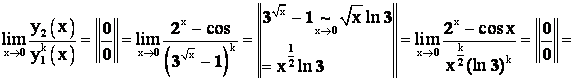
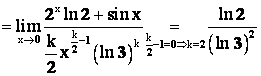
Ответ: ![]() – бесконечно малая функция 2-го порядка относительно бесконечно малой функции
– бесконечно малая функция 2-го порядка относительно бесконечно малой функции ![]() .
.
| < Предыдущая | Следующая > |
|---|