6.5 Вычисление пределов с помощью правила Лопиталя
Правило Лопиталя для раскрытия неопределенностей вида ![]() И
И ![]() сформулировано в виде теоремы:
сформулировано в виде теоремы:
Теорема. Пусть функции ![]() и
и ![]() дифференцируемы всюду в некоторой окрестности точки
дифференцируемы всюду в некоторой окрестности точки ![]() , т. е. при
, т. е. при ![]() , причем
, причем ![]() , тогда, если существует предел (конечный или бесконечный) отношения производных, то отношение функций имеет тот же предел, т. е.
, тогда, если существует предел (конечный или бесконечный) отношения производных, то отношение функций имеет тот же предел, т. е.
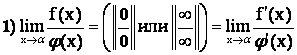

Обратите внимание на то, что существование предела отношения производных гарантирует существование предела отношения функций. Обратное утверждение неверно: предел отношения функций может существовать при отсутствии предела отношения производных.
Если на пример:
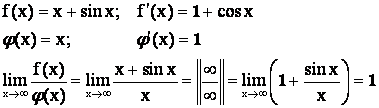
 - не существует.
- не существует.
Пример 1.
 .
.
Пример 2.
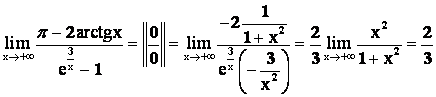 .
.
Правило Лопиталя может быть применено последовательно несколько раз, если отношение производных снова приводит к неопределенности, а сами производные удовлетворяют условиям применимости правила Лопиталя.
Пример 3.

Пример 4.

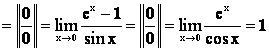 .
.
Раскрытие неопределенностей вида ![]() и
и ![]() проводят с помощью тождественных преобразований, которые переводят эти неопределенности к виду
проводят с помощью тождественных преобразований, которые переводят эти неопределенности к виду ![]() И
И ![]() , а затем применяют таблицу эквивалентных бесконечно малых величин и правило Лопиталя.
, а затем применяют таблицу эквивалентных бесконечно малых величин и правило Лопиталя.

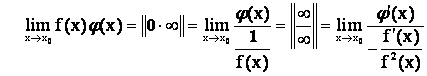
Пример 5.
 .
.
Пример 6.
A) 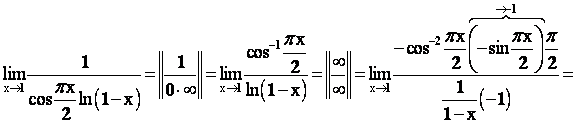
 .
.
Б) 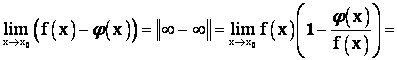
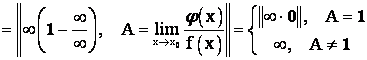
Пример 7.

Пример 8.
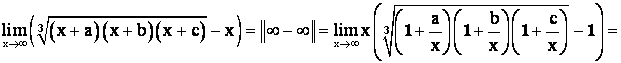

![]()
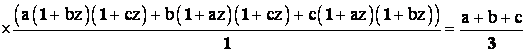
Пример 9.
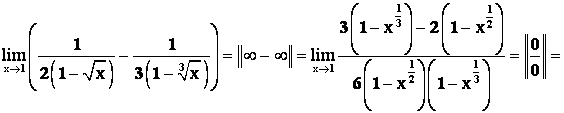



Раскрытие неопределенностей вида ![]() проводят с предварительным преобразованием степенно-показательного выражения по основному логарифмическому тождеству
проводят с предварительным преобразованием степенно-показательного выражения по основному логарифмическому тождеству ![]() к неопределённости
к неопределённости ![]() . Неопределённость
. Неопределённость ![]() легко приводится к неопределённостям
легко приводится к неопределённостям ![]() или
или ![]() . Тот или другой тип неопределённости выбирают имея в виду, что для применения правила Лопиталя числитель и знаменатель дроби нужно будет дифференцировать
. Тот или другой тип неопределённости выбирают имея в виду, что для применения правила Лопиталя числитель и знаменатель дроби нужно будет дифференцировать
При вычислении пределов обычно Совмещают применение эквивалентных бесконечно малых с Правилом Лопиталя. Все множители, стремящиеся к конечным пределам, отличным от нуля, сразу же заменяют этими пределами.
Пример 1.

Пример 2.


Пример 3.

Пример 4.

 .
.
Пример 5.

Замечание. Существует ряд пределов, в которых неопределенность может быть устранена только с помощью правила Лопиталя.
Приведем некоторые из них.
Пример 1.
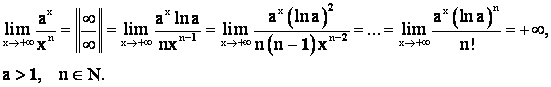
Здесь правило Лопиталя применено N раз.
Пример 2.

![]()
| < Предыдущая | Следующая > |
|---|