39. Парное уравнение регрессии
Задачи регрессионного анализа:
1. установление вида функции регрессии Y=F(X), описывающей зависимость результативного признака Y от факторного признака X (задача Структурной идентификации);
2. оценивание параметров функции регрессии (задача Параметрической идентификации);
3. использование полученного уравнения регрессии для прогнозирования значений результативного признака Y при различных значениях фактора X.
Наиболее сложным является решение задачи структурной идентификации регрессионной модели, когда необходимо определить с точностью до параметров математическую функцию, которая лучше других описывает взаимосвязь исследуемых признаков. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляться эмпирически – перебором и оценкой функций разных типов и т. п.
Для описания влияния факторного признака X на результативный признак Y в случае линейной зависимости строится Регрессионная модель вида
![]() , I=1, …, N, (8.14)
, I=1, …, N, (8.14)
Где N – число наблюдений; A0, A1 – неизвестные параметры уравнения регрессии; EI – случайная ошибка I-го наблюдения.
Уравнение Однофакторной (парной) линейной регрессии имеет вид:
![]() , (8.15)
, (8.15)
Где ![]() – теоретические значения результативного признака, полученные после подстановки Xi в уравнение регрессии; A0, A1 – оценки параметров уравнения регрессии.
– теоретические значения результативного признака, полученные после подстановки Xi в уравнение регрессии; A0, A1 – оценки параметров уравнения регрессии.
Оценки параметров уравнения A0, A1 можно найти с помощью Метода наименьших квадратов. Его суть заключается в том, что оценки параметров A0, A1 находят, минимизируя сумму квадратов отклонений эмпирических данных Yi от теоретических ![]() , рассчитанных по уравнению регрессии
, рассчитанных по уравнению регрессии
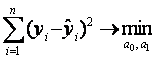 . (8.16)
. (8.16)
Для нахождения минимума данной функции ее частные производные приравнивают нулю и получают систему нормальных уравнений:

Отсюда
 (8.17)
(8.17)
E Если уравнение парной регрессии имеет более общий вид ![]() , где F(×) – некоторая аналитическая функция, то, проведя подстановку
, где F(×) – некоторая аналитическая функция, то, проведя подстановку ![]() , можно свести это уравнение нелинейной регрессии к линейному уравнению.
, можно свести это уравнение нелинейной регрессии к линейному уравнению.
Коэффициент регрессии A1 характеризует влияние, которое оказывает изменение фактора X на результативный признак Y. Он показывает, на сколько единиц в среднем изменится величина результативного признака Y при изменении факторного признака X на единицу.
Для удобства интерпретации коэффициента регрессии A1 используют Коэффициент эластичности, который показывает, на сколько процентов изменится величина результативного признака при изменении факторного признака на 1%:
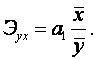 (8.18)
(8.18)
Для проверки гипотезы о значимости параметров регрессии A0, A1 можно использовать T-критерий Стьюдента. Для этого рассчитывают значения T-критерия по формулам
 (8.19)
(8.19)
Если ![]() , то гипотеза о том, что A0=0 (A1=0) отвергается при уровне значимости A. Значение TКр берется из таблицы распределения Стьюдента при уровне значимости A и числе степеней свободы N–2.
, то гипотеза о том, что A0=0 (A1=0) отвергается при уровне значимости A. Значение TКр берется из таблицы распределения Стьюдента при уровне значимости A и числе степеней свободы N–2.
Для оценки достоверности построенного уравнения регрессии можно использовать коэффициент детерминации ![]() , показывающий какая доля общей вариации результативного признака Y обусловлена воздействием факторного признака X. Чем ближе коэффициент детерминации к 1, тем лучше уравнение регрессии описывает зависимость Y от X.
, показывающий какая доля общей вариации результативного признака Y обусловлена воздействием факторного признака X. Чем ближе коэффициент детерминации к 1, тем лучше уравнение регрессии описывает зависимость Y от X.
| < Предыдущая | Следующая > |
|---|