40. Примеры решения задач 8
Пример 8.1. На основании следующих данных рассчитать:
|
Стоимость основных |
38 |
72 |
61 |
15 |
93 |
68 |
60 |
57 |
95 |
14 |
|
Производство продукции, млн руб. |
309 |
653 |
432 |
95 |
749 |
413 |
305 |
518 |
480 |
75 |
А) линейный коэффициент корреляции;
Б) коэффициент Фехнера;
В) коэффициенты ранговой корреляции Спирмэна и Кендалла.
Проверить значимость линейного коэффициента корреляции при уровне значимости 0,05. Построить доверительный интервал для линейного коэффициента корреляции при доверительной вероятности 0,90.
1) В таблице приведены промежуточные результата расчета коэффициента корреляции.
|
№ |
X |
Y |
|
|
|
|
|
|
1 |
38 |
309 |
–19,2 |
–93,9 |
368,64 |
8817,21 |
1802,88 |
|
2 |
72 |
653 |
14,8 |
250,1 |
219,04 |
62550,01 |
3701,48 |
|
3 |
60 |
432 |
2,8 |
29,1 |
7,84 |
846,81 |
81,48 |
|
4 |
15 |
95 |
–42,2 |
–307,9 |
1780,84 |
94802,41 |
12993,38 |
|
5 |
93 |
749 |
35,8 |
346,1 |
1281,64 |
119785,2 |
12390,38 |
|
6 |
68 |
413 |
10,8 |
10,1 |
116,64 |
102,01 |
109,08 |
|
7 |
60 |
305 |
2,8 |
–97,9 |
7,84 |
9584,41 |
–274,12 |
|
8 |
57 |
518 |
–0,2 |
115,1 |
0,04 |
13248,01 |
–23,02 |
|
9 |
95 |
480 |
37,8 |
77,1 |
1428,84 |
5944,41 |
2914,38 |
|
10 |
14 |
75 |
–43,2 |
–327,9 |
1866,24 |
107518,4 |
14165,28 |
|
Итого |
572 |
4029 |
7077,6 |
423198,9 |
47861,2 |
Средние арифметические: для признака X 
=572/10=57,2; для признака Y 
=4029/10=402,9.
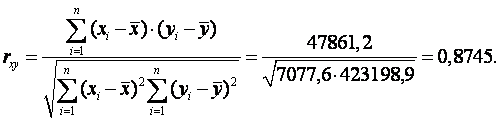
Согласно шкале Чэддока мы можем говорить о существовании Тесной корреляционной связи между исследуемыми признаками.
2) В таблице приведены промежуточные результата расчета коэффициента Фехнера.
|
№ |
X |
Y |
|
|
|
|
|
1 |
38 |
309 |
–19,2 |
–93,9 |
–1 |
–1 |
|
2 |
72 |
653 |
14,8 |
250,1 |
1 |
1 |
|
3 |
60 |
432 |
2,8 |
29,1 |
1 |
1 |
|
4 |
15 |
95 |
–42,2 |
–307,9 |
–1 |
–1 |
|
5 |
93 |
749 |
35,8 |
346,1 |
1 |
1 |
|
6 |
68 |
413 |
10,8 |
10,1 |
1 |
1 |
|
7 |
60 |
305 |
2,8 |
–97,9 |
1 |
–1 |
|
8 |
57 |
518 |
–0,2 |
115,1 |
–1 |
1 |
|
9 |
95 |
480 |
37,8 |
77,1 |
1 |
1 |
|
10 |
14 |
75 |
–43,2 |
–327,9 |
–1 |
–1 |
Число пар совпадающих знаков разностей (
) и (
) С =8.
Число пар несовпадающих знаков разностей () и () Н=2.
3) В таблице приведены промежуточные результаты расчета коэффициентов ранговой корреляции Спирмэна и Кендалла.
В таблице приведены пары (Xi, Yi), проранжированные в порядке возрастания признака X. Затем вместо значений Xi и Yi используются их ранги Rxi и Ryi.
E Так как значение признака X равное 60 встретилось дважды, поэтому каждому из этих значений приписывают ранг, равный среднему арифметическому порядковых номеров объектов, т. е. (5+6)/2=5,5.
Тогда коэффициент ранговой корреляции Спирмэна равен
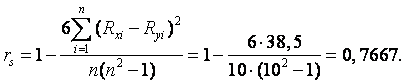
4) Для расчета коэффициента ранговой корреляции Кендалла используется только колонка с рангами значений признака Y. Например, Sign(Ry2–Ry1)=Sign(2–1)=1 (ячейка, куда занесено полученное значение, выделена серым цветом). В результате получим
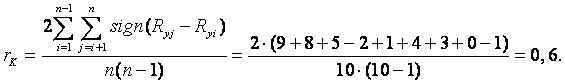5) Для проверки значимости коэффициента корреляции рассчитаем значение T-критерия Стьюдента
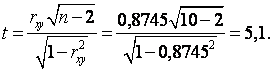
Так как выполняется неравенство 
(5,1>TКр=2,306), то гипотеза о том, что коэффициент корреляции Rxy=0 отвергается при уровне значимости 0,05. Табличное значение TКр=2,306 было найдено по таблице (см. приложение) при A=1–0,05=0,95 (здесь 0,05 – это заданный уровень значимости) и числе степеней свободы 10–2=8.
6) Для построения доверительного интервала коэффициента корреляции выполним Z-преобразование Фишера
Средняя ошибка величины Z 
Доверительный интервал для Z имеет вид [Z–T×SZ; Z+T×SZ], Значение T=1,6449 находим по таблице в приложении при доверительной вероятности A=0,90 и числе степеней свободы ¥. Тогда доверительный интервал для Z [1,352–1,6449× 0,378; 1,352+1,6449× 0,378] или [0,7303; 1,974].
Выполнив обратное z-преобразование Rxy=tanh(Z), получим доверительный интервал для коэффициента корреляции Rxy: [tanh(0,7303); tanh(1,974)] или [0,6232; 0,9621].
Пример 8.2. Рассчитайте коэффициент ассоциации Юла-Кендэла и коэффициент контингенции Пирсона между показателями доходов родителей и их детей.
|
Доходы детей ниже среднего |
Доходы детей выше среднего | |
|
Доходы родителей ниже среднего |
37 |
28 |
|
Доходы родителей выше среднего |
12 |
64 |
Коэффициент ассоциации 
Коэффициент контингенции
Таким образом, между доходами родителей и их детей имеется существенная связь.
Пример 8.3. Респонденты в ходе опроса давали ответ на два вопроса. Оцените взаимосвязь полученных ответов на вопросы анкеты.
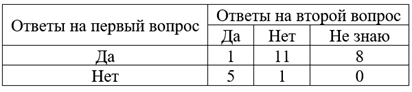
Решение. На основе приведенной таблицы распределения определим: K1=2, K2=3 – число возможных ответов на первый и второй вопросы соответственно; Mi, Nj – итоговые частоты соответствующего столбца и строки.
Отсюда показатель взаимной сопряженности J 2
.
Тогда коэффициент взаимной сопряженности Пирсона
.
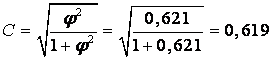Коэффициент взаимной сопряженности Чупрова
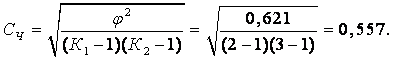
Таким образом, в соответствии со шкалой Чэддока можно говорить о существовании заметной связи между ответами респондентов на вопросы.
Пример 8.4. На основании данных примера 8.1: 1) оцените параметры уравнения парной регрессии; 2) оцените достоверность уравнения регрессии с помощью коэффициента детерминации; 3) проверьте гипотезы о значимости параметров уравнения парной регрессии при уровне значимости 0,05; 4) постройте диаграмму рассеяния и линию уравнения парной регрессии; 5) рассчитайте коэффициент эластичности.
Решение.
1) Для оценки параметра A0 найдем среднеквадратическое отклонение признаков X и Y.
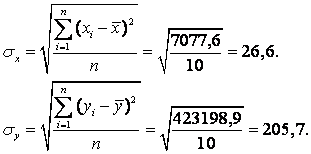
Тогда оценки параметров уравнения регрессии
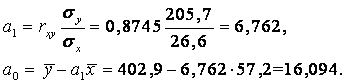
2) Коэффициент детерминации 
. Таким образом, различия в объемах производства продукции на 76,48% определяются величиной основных фондов предприятия, а на 23,52% – влиянием прочих факторов.
3) Для проверки гипотезы о значимости параметров уравнения парной регрессии рассчитаем значения T-критерия
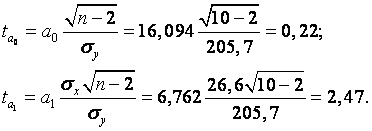
Табличное значение TКр=2,306 при уровне значимости 0,05 и числе степеней свободы 10–2=8 (см. таблицу распределения Стьюдента в приложении для A=1–0,05=0,95). Так как неравенство 
не выполняется, то мы не можем отвергнуть гипотезу о том, что параметр A0=0. Неравенство же 
выполняется, поэтому мы отвергаем гипотезу, что параметр A1=0. Таким образом, можно сделать вывод, что в данной регрессионной модели значим только параметр A1, и уравнение регрессии должно иметь вид 
.
4) На рис. 8.3 приведена диаграмма рассеяния для признаков X и Y. На диаграмме рассеяния проведена линия уравнения парной регрессии и указано значение коэффициента детерминации.
Рис. 8.3. Диаграмма рассеяния
5) Коэффициент эластичности равен 
Таким образом, при увеличении стоимости основных фондов на 1% производство продукции в среднем возрастает на 0,96%.
| < Предыдущая | Следующая > |
|---|
