38. Измерение тесноты корреляционной связи двух качественных признаков
Для измерения тесноты связи между качественными признаками могут быть использованы коэффициенты ранговой корреляции при условии, что значения признаков могут быть проранжированы (упорядочены) в порядке убывания или возрастания.
Для расчета ранговых коэффициентов корреляции необходимо упорядочить пары значений (Xi, Yi), например, в порядке возрастания для признака Х. Затем значения Xi,, Yi заменяют их рангами Rxi, RyI. Ранг – это порядковый номер объекта в ранжированном ряде. Если объекты имеют одинаковое значение признака, то каждому из них приписывают ранг, равный среднему арифметическому порядковых номеров объектов.
1) Коэффициент ранговой корреляции Спирмэна
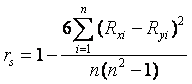 . (8.7)
. (8.7)
2) Коэффициент ранговой корреляции Кендалла.
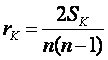 , (8.8)
, (8.8)
Где 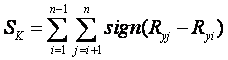 ;
; 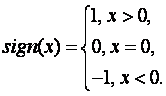
Отметим, что ранговые коэффициенты корреляции принимают значения в интервале от –1 до +1. Кроме того, они позволяют измерять тесноту связи не только качественных, но и количественных признаков.
Если качественные признаки являются альтернативными, принимающими только два взаимоисключающих значения, то для определение тесноты связи могут быть использованы:
3) Коэффициент ассоциации Юла-Кендэла.
4) Коэффициент контингенции Пирсона.
Рассмотрим четырехклеточную корреляционную таблицу (таблицу «четырех полей») с частотами A, B, C, D.
|
Признак Y – да |
Признак Y – нет | |
|
Признак X – да |
A |
B |
|
Признак X – нет |
C |
D |
Коэффициент ассоциации имеет вид
![]() . (8.9)
. (8.9)
Коэффициент контингенции выражается формулой
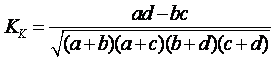 . (8.10)
. (8.10)
Коэффициенты ассоциации и контингенции изменяются от –1 до +1. Выполняется неравенство ½KА½³½KK½. Таким образом, коэффициент ассоциации завышает значение корреляции. Связь считается существенной, если ½KK½³0,3 или ½KА½³0,5.
Если качественный признак представлен более чем двумя группами, то можно использовать:
5) Коэффициент взаимной сопряженности Пирсона.
6) Коэффициент взаимной сопряженности А. А Чупрова.
Для расчета коэффициентов взаимной сопряженности необходимо рассчитать показатель взаимной сопряженности J 2
 , (8.11)
, (8.11)
Где K1, K2 – число возможных значений X и Y соответственно; Fij – частота клетки в таблице распределения; Mi, Nj – итоговые частоты соответствующих строк и столбцов, 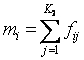 ,
, 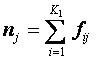 (см. пример 8.3).
(см. пример 8.3).
Тогда Коэффициент взаимной сопряженности Пирсона
 . (8.12)
. (8.12)
Коэффициент взаимной сопряженности Чупрова
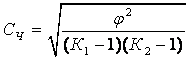 . (8.13)
. (8.13)
| < Предыдущая | Следующая > |
|---|