37. Методы измерения корреляционной связи. Измерение тесноты корреляционной связи двух количественных признаков
Для измерения тесноты (силы) связи двух количественных показателей могут применяться следующие показатели.
1) Линейный коэффициент корреляции Пирсона
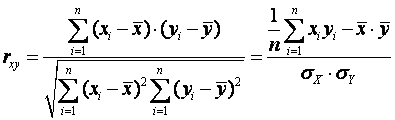 . (8.1)
. (8.1)
Он принимает значения в интервале от –1 до +1. Если величины Y и X независимы, то коэффициент корреляции Rxy=0. Положительные значения Rxy указывают на прямую связь, отрицательные – на обратную. Если Rxy=±1, то Y и X связаны линейной функциональной зависимостью Y=A0+A1X.
На рис. 8.1 приведены примеры диаграмм рассеяния пар значений X и Y. Случаи а), б) и в) наглядно демонстрируют, что коэффициент корреляции Rxy позволяет измерить именно линейную корреляционную связь. Напротив, случаи г) и д) показывают, что когда признаки X и Y связаны нелинейно, использование Линейного коэффициента корреляции Rxy некорректно.
Для проверки гипотезы о существенности (значимости) коэффициента корреляции можно использовать T-критерий Стьюдента. Для этого рассчитывают значение T-критерия по формуле
 (8.2)
(8.2)
Если ![]() , то гипотеза о том, что Rxy=0 отвергается при уровне значимости A. Значение TКр берется из таблицы распределения Стьюдента при уровне значимости A и числе степеней свободы N–2.
, то гипотеза о том, что Rxy=0 отвергается при уровне значимости A. Значение TКр берется из таблицы распределения Стьюдента при уровне значимости A и числе степеней свободы N–2.
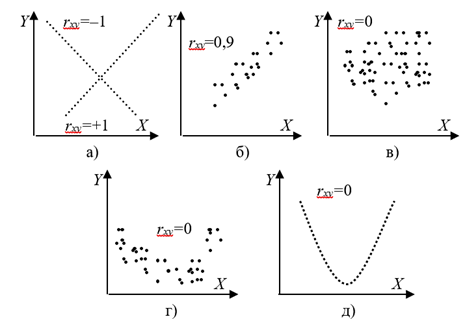
Рис. 8.1. Примеры диаграмм рассеяния признаков X и Y и соответствующих коэффициентов корреляции
Для расчета доверительного интервала оценки коэффициента корреляции можно использовать Z-преобразование Р. Фишера
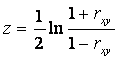 (8.3)
(8.3)
Величина z имеет приблизительно нормальное распределение, поэтому доверительный интервал для Z имеет вид [Z–T×SZ, Z+T×SZ], где SZ – средняя ошибка величины Z.
![]() . (8.4)
. (8.4)
Коэффициент доверия T находят из таблицы распределения Стьюдента при заданной доверительной вероятности A и числе степеней свободы ¥. Обратный пересчет Z в RXy производят по формуле
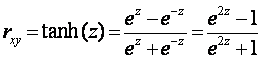 , (8.5)
, (8.5)
Где tanh(×) – гиперболический тангенс.
Все выше изложенное справедливо, если совместное распределение X и Y является нормальным.
Для качественной характеристики силы связи может использоваться шкала Чэддока (см. п.4.3).
2) Коэффициент детерминации H2 и Выборочное корреляционное отношение H.
Для оценки тесноты Линейной корреляционной связи служит коэффициент корреляции Rxy. Для оценки тесноты Нелинейной корреляционной связи можно использовать выборочное корреляционное отношение Y к X
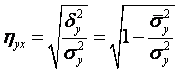 , (8.6)
, (8.6)
где ![]() – межгрупповая дисперсия признака Y;
– межгрупповая дисперсия признака Y; ![]() – внутригрупповая дисперсия;
– внутригрупповая дисперсия; ![]() – общая дисперсия (см. п.4.3).
– общая дисперсия (см. п.4.3).
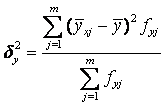 ,
, 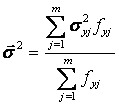 ,
, 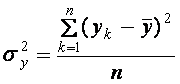 ,
, 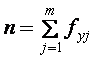 .
.
Аналогично определяется выборочное корреляционное отношение Х к Y
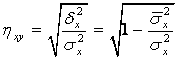 .
.
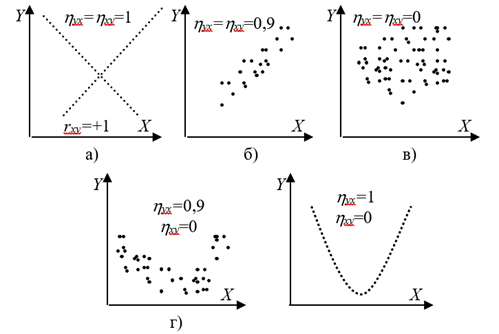
Рис. 8.1. Примеры диаграмм рассеяния признаков X и Y и соответствующих корреляционных отношений
Свойства выборочного корреляционного отношения HYx.
1. ![]() .
.
2. Если ![]() , то признак Y с признаком Х корреляционной зависимостью не связан.
, то признак Y с признаком Х корреляционной зависимостью не связан.
3. Если ![]() , то признак Y связан с признаком Х функциональной зависимостью.
, то признак Y связан с признаком Х функциональной зависимостью.
4. ![]() .
.
5. Если ![]() , то имеет место точная линейная корреляционная зависимость.
, то имеет место точная линейная корреляционная зависимость.
3) Коэффициент Фехнера
![]() ,
,
Где С – число пар совпадающих знаков разностей (![]() ) и (
) и (![]() ); Н – число пар несовпадающих знаков.
); Н – число пар несовпадающих знаков.
| < Предыдущая | Следующая > |
|---|