19. Оптимальный объем выборки

Размер ошибки выборки прежде всего зависит от объема выборочной совокупности N. Средняя ошибка выборки обратно пропорциональна (например, при увеличении объема выборки в четыре раза, ее ошибка уменьшается в только в два раза). Таким образом, увеличение объема выборки приводит к снижению ошибки выборки, но, с другой стороны, вызывает дополнительные расходы на проведение исследования.

При планировании выборочного наблюдения обычно заранее задают допустимую ошибку выборки и доверительную вероятность, чтобы обеспечить заданную точность результатов наблюдения.

Найдем оптимальный объем выборки для нахождения выборочной средней (случайный повторный отбор) при заданных предельной ошибке выборки и доверительной вероятности A. Согласно (5.4) и (5.8)

.

Отсюда оптимальный объем выборки N

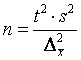. (5.10)

В таблице приведены формулы для расчета оптимального размера выборки (случайный отбор).

Эти формулы должны использоваться на этапе планирования выборочного наблюдения, однако в них необходимо указывать неизвестные нам значения выборочной дисперсии S2 и выборочной доли W. Вместо них на практике рекомендуется использовать какие-либо приближенные оценки этих характеристик (например, полученные в результате пробных выборочных наблюдений или из предыдущих обследований аналогичной совокупности). Кроме того, часто неизвестное значение W заменяют значением 0,5. Если известна примерная величина генеральной средней, то иногда используют приближенную формулу 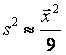. Если известна примерная величина размаха совокупности, то можно использовать приближенную формулу .

E Эти приближенные формулы можно использовать ТОЛЬКО ПРИ ОТСУТСТВИИ БОЛЕЕ ТОЧНЫХ ДАННЫХ, полученных в результате пробных выборочных обследований или из предыдущих обследований аналогичной совокупности.

E При больших размерах генеральной совокупности оптимальный объем выборки при повторном и бесповторном отборе отличаются незначительно.

< Предыдущая		Следующая >