20. Примеры решения задач 5
Пример 5.1. При выборочном обследовании (отбор случайный бесповторный) 25 деталей из общей партии в 400 деталей было обнаружено две бракованных детали.
Найдите доверительный интервал с доверительной вероятностью 0,95 для доли бракованных деталей. Укажите доверительный интервал для числа бракованных деталей в партии.
Выборочная доля бракованных деталей 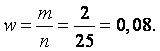
Средняя ошибка выборки

Коэффициент доверия T при доверительной вероятности A=0,95 и объеме выборки N=25 равен 2,0595 (см. приложение).
Предельная ошибка выборки ![]()
Доверительный интервал для генеральной доли
![]()
Доверительный интервал для числа бракованных деталей в партии
![]()
По смыслу задачи отрицательные значения нижней границы недопустимы, поэтому откорректируем их с учетом имеющихся данных.
Доверительный интервал для числа бракованных деталей
![]()
Доверительный интервал для генеральной доли
![]()
E Этот парадоксальный результат (отрицательные значения нижней границы доверительного интервала) связан с тем, что в условиях малых выборок используемые формулы не в полной мере отражают особенности распределения выборочных значений.
Пример 5.2.
При выборочном обследовании выполнения рабочими норм времени были получены следующие данные:
|
Выполнение норм времени, % |
До 96 |
96–98 |
98–100 |
100–102 |
102 и более |
|
Число рабочих |
2 |
5 |
11 |
17 |
5 |
Определите доверительный интервал для среднего процента выполнения норм времени (доверительная вероятность 0,99). Всего на предприятии работает 1000 рабочих.
|
Выполнение норм времени, % |
Число рабочих, Fi |
Середина интервала, Xi |
Xi× fi |
|
|
|
До 96 |
2 |
95 |
190 |
24,01 |
48,02 |
|
96–98 |
5 |
97 |
485 |
8,41 |
42,05 |
|
98–100 |
11 |
99 |
1089 |
0,81 |
8,91 |
|
100–102 |
17 |
101 |
1717 |
1,21 |
20,57 |
|
102 и более |
5 |
103 |
515 |
9,61 |
48,05 |
|
Итого |
40 |
3996 |
167,6 |
Выборочная средняя ![]() =3996/40=99,9%.
=3996/40=99,9%.
Выборочная дисперсия S2=167,6/40=4,19.
Средняя ошибка выборки
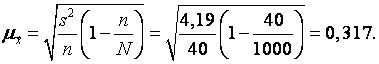
Коэффициент доверия T при доверительной вероятности A=0,99 и объеме выборки N=40 равен 2,7045 (см. приложение).
Предельная ошибка выборки
![]()
Доверительный интервал для генеральной средней
![]()
Пример 5.3.
При обследовании месторождения золота было взято 100 проб. Среднее содержание золота составило 2,4 г/куб. м при среднем квадратическом отклонении 0,4 г/куб. м. Найти доверительный интервал для среднего содержания золота в породах месторождения (доверительная вероятность 0,9). Спрогнозировать потенциальные запасы золота на месторождении, если объем золотосодержащих пород оценивается в 20 млн. куб. м.
Решение.
Так как выборка является гипотетической, то объем генеральной совокупности N=¥. Отсюда средняя ошибка выборки
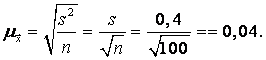
Коэффициент доверия T при доверительной вероятности A=0,9 и объеме выборки N=100 равен 1,6602 (см. приложение).
Предельная ошибка выборки
![]() Г/куб. м.
Г/куб. м.
Доверительный интервал для генеральной средней
![]()
Прогноз запасов золота на месторождении (в тоннах)
![]()
Пример 5.4. С целью определения средних затрат времени при поездках на работу планируется провести опрос сотрудников предприятия на основе случайного бесповторного отбора. Оцените необходимый объем выборочной совокупности, чтобы с вероятностью 0,95 ошибка выборочной средней не превышала 1 минуты. На предприятии работает 2000 человек.
Решение. Так как нам неизвестна выборочная дисперсия изучаемого признака, попробуем приблизительно оценить ее. Выскажем предположение, что в среднем работники затрачивают на одну поездку 30 минут. Используем одну из приближенных формул для оценки выборочной дисперсии

Положим коэффициент доверия T при доверительной вероятности A=0,95 равным 1,96, так как объем выборки N нам неизвестен..
Тогда необходимый объем выборочной совокупности
 человека.
человека.
| < Предыдущая | Следующая > |
|---|