18. Ошибки выборки и доверительные интервалы

Значение обобщающего показателя, рассчитанное по выборочной совокупности (выборке), может в той или иной мере отличаться от значения этого показателя в генеральной совокупности.

Ошибка выборки– это возможное расхождение между характеристиками выборочной и генеральной совокупности.

По выборочной совокупности обычно рассчитывают два вида обобщающих показателей.

1) Средняя величина количественного признака (Выборочная средняя ) – это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности. Например, средняя зарплата, средний рост, средний возраст и т. д.

2) Относительная величина альтернативного признака (Выборочная доля W) характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием (отсутствием) изучаемого признака. Например, доля бракованных изделий в партии, удельный вес женщин среди работников предприятия и т. д.

В генеральной совокупности среднюю величину количественного признака называют Генеральной средней (обозначается ), а долю единиц, обладающих изучаемым признаком, называют Генеральной долей (обозначается Р).

Выборочная средняя определяется по формуле средней арифметической.

Выборочная доля W (частость) определяется по формуле

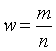, (5.1)

Где M – число единиц, обладающих изучаемым признаком, N – общая численность выборочной совокупности (Объем выборки).

Основная задача выборочного исследования – на основе характеристик выборочной совокупности w и получить достоверные суждения о показателях доли p и средней в генеральной совокупности.

Возможные расхождения между характеристиками выборочной и генеральной совокупностей измеряются средней ошибкой выборки μ.

В математической статистике доказывается, что При Случайном повторном отборе средние ошибки теоретически рассчитывают по формулам:

· для выборочной средней

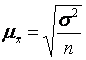, (5.2)

Где S2 – генеральная дисперсия;

· для выборочной доли W

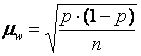. (5.3)

Но при проведении выборочных обследований генеральная дисперсия S2 и генеральная доля P, как правило, неизвестны. На практике вместо них используют оценки, полученные по выборочной совокупности.

Таким образом, на практике расчетные формулы для определения средней ошибки выборки При Случайном повторном отборе будут иметь вид:

· для выборочной средней

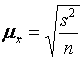, (5.4)

Где S2 – дисперсия, рассчитанная для выборочной совокупности (Выборочная дисперсия);

· для выборочной доли W

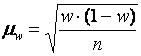. (5.5)

При случайном бесповторном отборе формулы средней ошибки выборки включают дополнительный множитель 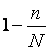и принимают следующий вид:

· для выборочной средней

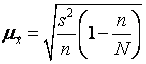; (5.6)

· для выборочной доли W

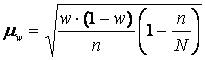. (5.7)

Значения средней ошибки выборки необходимы для установления диапазонов возможных значений генеральной доли P И генеральной средней , что позволяет указать доверительные интервалы:

· для генеральной средней ; (5.8)

· для генеральной доли P , (5.9)

Где – предельная ошибка выборки для генеральной средней; – предельная ошибка выборки для генеральной доли.

Коэффициент T – это Коэффициент доверия, зависящий от Доверительной вероятности A.

E Заметим, что генеральная характеристика ( или Р) нам неизвестна, и мы лишь можем утверждать, что с доверительной вероятностью A генеральная характеристика принадлежит доверительному интервалу (т. е. с доверительной вероятностью доверительный интервал покроет или Р).

В общем случае значения коэффициента доверия T при заданной доверительной вероятности A и известном объеме выборки N можно найти с помощью таблиц распределения Стьюдента (см. приложение).

На практике для выборок достаточно большого объема (N³30) часто применяют следующие приближенные значения коэффициента доверия T без учета объема выборки N.

Доверительная вероятность A	0,90	0,95	0,954	0,990	0,9973
Коэффициент доверия T	1,645	1,9600	2,000	2,576	3,000

< Предыдущая		Следующая >