09. Средние структурные

Особым видом средних величин являются Структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения.

Порядок расчета средних структурных существенно отличается для дискретных и интервальных рядов распределения.

Мода – величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Мода отражает типичный, наиболее распространенный вариант значения признака.

В дискретном ряду распределения мода – это варианта, которой соответствует наибольшая частота.

В интервальном ряду распределения сначала определяют модальный интервал (т. е. интервал, содержащий моду), которому соответствует наибольшая частота. Конкретное значение моды определяется формулой:

, (3.9)

Где XMo – нижняя значение модального интервала; H – величина модального интервала; FMo – частота модального интервала; FMo-1 – частота интервала, предшествующего модальному; FMo+1 – частота интервала, следующего за модальным.

Моду можно определить графически по полигону (рис. 3.1, а) или гистограмме (рис. 3.1, б) распределения.

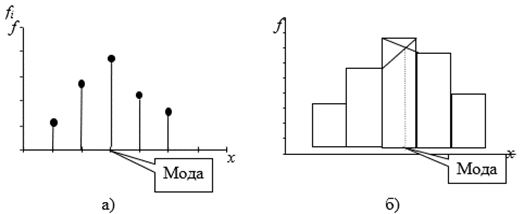
Рис. 3.1. Графическое определение моды по:
а) полигону дискретного ряда; б) гистограмме интервального ряда

Медиана – это варианта, находящаяся в середине ранжированного ряда (варианта, делящая ранжированный ряд пополам).

E Так как при расчете средних структурных часто используется ранжированный ряд, напомним, что Ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.

Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Если число вариант четное, то медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда.

Для дискретных и интервальных рядов используется кумулятивный ряд снизу (ряд накопленных частот). Кроме того, необходимо рассчитать половину общей суммы частот .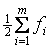

В дискретном ряду медианой является варианта, которой соответствует член кумулятивного ряда, впервые превысившая половину общей суммы частот.

В случае интервального ряда сначала необходимо определить медианный интервал (т. е. интервал, содержащий медиану). Медианным интервалом является тот, которому соответствует член кумулятивного ряда, впервые превысившая половину общей суммы частот. Затем конкретное значение медианы рассчитывают по формуле

, (3.10)

XMe – нижняя граница медианного интервала; H – Величина медианного интервала; SMe-1 – член кумулятивного ряда, предшествующий медианному интервалу; FMe – частота медианного интервал.

Графически медиану можно определить по кумуляте (рис.3.2).

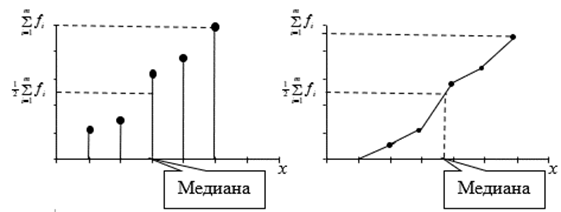
Рис. 3.2. Графическое определение медианы по кумуляте:
а) дискретного ряда; б) интервального ряда

Квартили делят ранжированный ряд на четыре части. Различают первый (нижний) квартиль, второй (центральный) квартиль (совпадает с медианой) и третий (верхний) квартиль.

Первый квартиль – это варианта ранжированного ряда, превышающая 1/4 единиц совокупности и меньшая, чем 3/4 единиц совокупности.

Третий квартиль – это варианта ранжированного ряда, превышающая 3/4 единиц совокупности и меньшая, чем 1/4 единиц совокупности.

Для интервального ряда квартили находят по формулам

(3.11)

Где Q1, Q3 – первый и третий квартили; XQ1, XQ3 – нижние границы квартильных интервалов; H – Величина квартильного интервала; SQ1-1, SQ3-1 – члены кумулятивного ряда, предшествующие квартильному интервалу; FQ1, FQ3 – частоты квартильных интервалов.

Квартили также можно определить по кумуляте (рис.3.3).

Рис. 3.3. Графическое определение квартилей по кумуляте:
а) дискретного ряда; б) интервального ряда

Децили делят ранжированный ряд на десять равных частей. Всего возможно 9 децилей. Например, первый дециль превышает 1/10 единиц совокупности и меньше, чем 9/10 единиц совокупности.

В случае интервального ряда децили Dj рассчитывают по формуле

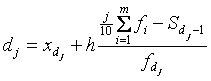, J=1,…, 9, (3.12)

Где Xdj – нижние границы децильных интервалов; H – Величина децильного интервала; – член кумулятивного ряда, предшествующий децильному интервалу; – частота децильного интервала.

Перцентили (процентиль) делят ранжированный ряд на десять равных частей. Всего возможно 99 перцентилей. Например, седьмой перцентиль превышает 7/100 единиц совокупности и меньше, чем 93/100 единиц совокупности.

Нахождение децилей и перцентилей возможно сделать графически на основе кумуляты по аналогии с медианой и квартилями.

На практике наиболее часто из средних структурных используют моду и медиану.

< Предыдущая		Следующая >