10. Примеры решения задач 3

Пример 3.1. Каждый из 5 рабочих бригады изготовил за смену 35, 28, 31, 29, 33 изделий. Рассчитать среднюю выработку одного работника.

Решение. Средняя выработка, характеризующая производительность труда, рассчитывается в данном случае как средняя арифметическая простая, так как данные не сгруппированы.

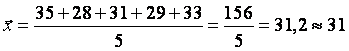изделие.

Пример 3.2. Рассчитать среднее число работников на одном предприятии.

Распределение предприятий по числу работников (чел.)

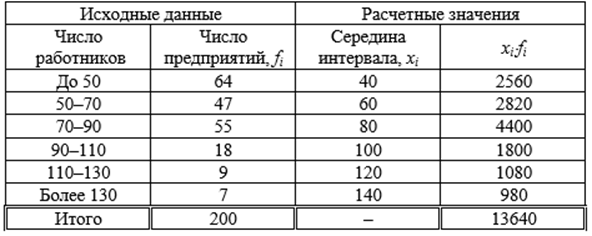
Решение. Ряд распределения предприятий представлен в виде интервального ряда, поэтому при расчетах необходимо использовать среднюю арифметическую взвешенную. От интервального ряда перейдем дискретному ряду путем замены интервальных значений их средними значениями. При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний).

Тогда среднее число работников на одном предприятии

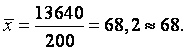
Пример 3.3. Имеется информация о трех сделках по продаже обыкновенных акций одного предприятия. Рассчитать средний курс акций по этим сделкам.

№ п/п	Курс акций, руб.	Сумма сделки, тыс. руб.
1	28,30	4245
2	28,75	2300
3	28,55	2855
Итого		9400

Решение. В приведенных данных отсутствует информация о количестве проданных акций, т. е. не известны частоты Fi. Однако, зная суммы сделок и курсы акций по каждой сделке, мы можем рассчитать количество проданных акций. В данном случае для расчета среднего курса акций применим формулу средней гармонической взвешенной.

руб.

Пример 3.4. Двое рабочих в течение смены заняты изготовлением одинаковых деталей. Один рабочий тратит на изготовление детали 3 минуты, другой – 4,5 мин. Определить средние затраты времени на изготовление детали.

Решение. На первый взгляд, следует применить формулу средней арифметической простой, но в течение смены рабочими было изготовлено разное число деталей. Средние затраты времени на одну деталь должны определяться как отношение суммарные затраты времени к общему количеству изготовленных деталей.

Затраты времени представляют собой произведение количества изготовленных деталей (Fi) и времени на изготовление одной детали (Xi). Поскольку затраты рабочего времени (X×IFi) у обоих рабочих равны (смена), то применим формулу средней гармонической простой.

Мин.

Пример 3.5. Решить задачу 3.4 при условии, что 1-й рабочий отработал 6 часов, а 2-й рабочий – 2 часа.

Решение. В этом случае применим формулу средней гармонической взвешенной.

Мин.

Пример 3.6. По имеющимся данным о ценах товара в различных фирмах города определить моду и медиану.

А) 25,6 24,3 23,8 25,7 24,3

Б) 25,6 24,3 23,8 25,7 24,3 24,9

Решение. В обоих случаях данные не сгруппированы.

А) в данной совокупности чаще всего повторяется значение 24,3, поэтому Мо=24,3.

Для определения медианы надо провести ранжирование:

23,8 24,3 24,3 25,6 25,7

В данном ряду нечетное число членов (5), поэтому варианта, расположенная посередине, является медианой. Ме=24,3.

Б) в данной совокупности чаще всего повторяется значение 24,3, поэтому Мо=24,3.

Для определения медианы проведем ранжирование:

23,8 24,3 24,3 24,9 25,6 25,7

В данном ряду четное число членов (6), поэтому медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда, т. е. Ме=(24,3+24,9)/2=24,6.

Пример 3.7. По имеющимся данным о сбыте продукции (в тыс. руб.) в различных фирмах города определить: средний объем сбыта, моду, медиану, квартили.

87, 75, 66, 60, 87, 67, 66, 69, 89, 74, 90, 78, 99, 86, 76, 95, 69, 68, 87, 63.

Решение. Поскольку представленные 20 значений признака не сгруппированы, то применим формулу средней арифметической простой.

Наиболее часто в совокупности встречается значение 87 (частота F=3), поэтому мода равна 87.

Для определения медианы и квартилей необходимо провести ранжирование. Ниже приведен полученный ранжированный ряд.

60, 63, 66, 66, 67, 68, 69, 69, 74, 75, 76, 78, 86, 87, 87, 87, 89, 90, 95, 99.

В данном ряду четное число членов (20), поэтому медиана рассчитывается как средняя арифметическая из двух вариант, расположенных в центре ряда, т. е. Ме=(75+76)/2=75,5.

Чтобы определить первый квартиль, отсчитаем в ранжированном ряду 5 (¼×20) наименьших значений признака. Таким образом, 1-й квартиль, превышающий 5 наименьших значений, можно найти как среднюю арифметическую Q1=(67+68)/2=67,5.

E Можно убедиться, что ¼ единиц совокупности меньше 67,5 и ¾ единиц больше 67,5.

Второй квартиль совпадает с медианой.

Для нахождения третьего квартиля необходимо найти 15 (¾×20) наименьших значений признака. Тогда Q3=(87+87)/2=87.

E Приведем пример нахождения третьего дециля. Для этого найдем 6 (3/10×20) наименьших значений. Тогда D3=(68+69)/2=68,5.

Пример 3.8. Произвести группировку данных задачи 3.7, образовав 4 равных интервалов. По полученному интервальному ряду определить (аналитически и графически): средний объем сбыта, моду, медиану, квартили.

Решение. В таблице приведены результаты группировки исходных данных (величина интервала H=10).

Номер группы	Границы группы	Частота, Fi	Кумулятивный ряд, Si	Середина интервала, Xi	Xi× fi
1	До 70	8	8	65	520
2	70–80	4	12 (8+4)	75	300
3	80–90	3	15 (12+3)	85	255
4	Более 90	5	20 (15+5)	95	475
	Итого	20			1550

Для интервального ряда применим формулу средней арифметической взвешенной.

Чтобы найти моду, найдем модальный интервал с наибольшей частотой. Это 1-й интервал с частотой FMo=8. В качестве нижней границы 1‑го открытого интервала зададим 60, так как по условиям задачи при группировке использованы равные интервалы. Тогда

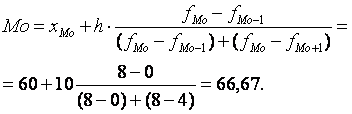
Для определения медианного интервала воспользуемся кумулятивным рядом, приведенным в таблице, и найдем, когда кумулятивный ряд в первый раз превысит половину общей суммы частот . Это случится во 2-м интервале, т. к. выполнится неравенство 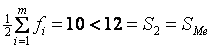. Таким образом, медианным интервалом оказался 2-й интервал. Тогда нижняя граница медианного интервала XMe=70; член кумулятивного ряда, предшествующий медианному интервалу, SMe-1=S1=8; частота медианного интервал FMe=F2=4 и

Для нахождения 1-го квартиля определим 1-й квартильный интервал, в котором впервые кумулятивный ряд превысит величину . Это случится уже в 1-м интервале, т. к. 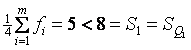. Тогда нижняя граница 1-го квартильного интервала; =60; член кумулятивного ряда, предшествующий 1-му квартильному интервалу, =S0=0; частота 1-го квартильного интервала =F1=8 и в итоге получим

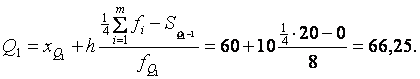
Аналогично найдем, что 3-й квартиль попал в 4-й интервал, т. к. в этом интервале выполняется 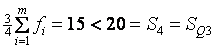. Тогда XQ3=90; член кумулятивного ряда, предшествующий 3-му квартильному интервалу, SQ3-1=S3=15; частота 4-го квартильного интервала FQ3=F3=5;

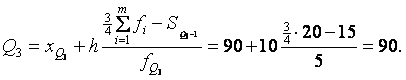
На рис.3.4. приведено графическое решение задачи нахождения моды, медианы и квартилей.

Рис. 3.4. Графическое определение:
а) моды; б) медианы и квартилей

E Приведем пример нахождения третьего дециля. Уже в 1-м интервале выполняется неравенство . Тогда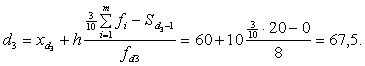

E Обратите внимание, что полученные значения средних величин отличаются в зависимости от того, какие данные (сгруппированные или несгруппированные) были использованы. Более точные результаты получаются для несгруппированных данных.

< Предыдущая		Следующая >