08. Средние величины

Метод средних – это метод исследования статистической совокупности путем измерения ее средних величин.

Идея метода средних – вместо исходной совокупности рассматривают ее заменяющую совокупность, в которой все единицы имеют одинаковое значение количественного признака. Этим достигается сопоставимость разных совокупностей, так как сравниваются не сами совокупности, а эти обобщающие показатели (средние).

Важнейшее свойство средней величины в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

Выделяют два основных класса средних:

1. средние степенные;

2. средние структурные;

Выбор той или иной формулы для расчета средней величины определяется экономическим содержанием исследуемого показатели и наличием соответствующей статистической информации.

1. Средние степенные

К числу средних степенных относятся:

1. средняя арифметическая;

2. средняя гармоническая;

3. средняя геометрическая;

4. средние степенные.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным, а взвешенная – по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения.

2. Средняя арифметическая.

Средняя арифметическая Простая.

, (3.1)

Где Хi – варианты совокупности; N – общая численность совокупности.

Средняя арифметическая Взвешенная.

, (3.2)

Где FI – частота варианты совокупности; M – число различных вариант совокупности. или частость

E Отметим, что в формуле (3.2) вместо частот FI можно использовать частости WI. При этом , .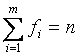

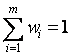В случае, если исходные данные представлены в виде интервального ряда распределения, то в качестве вариантов усредняемого признака (Хi) принимают середины интервалов, вычисляемые по каждой группе. Серединное значение интервала может определяться несколькими способами:

1) середина закрытого интервала = полусумма верхней и нижней границ интервала;

2) середина первого (открытого) интервала = середина второго интервала – величина второго интервала;

3) середина последнего (открытого) интервала = середина предпоследнего интервала + величина предпоследнего интервала.

3. Средняя гармоническая.

Средняя гармоническая простая

. (3.3)

Средняя гармоническая взвешенная

. (3.4)

Рассмотрим два примера.

Пример 1. Автомобиль от склада до магазина проезжает 20 км со скоростью 40 км/ч, а обратно на склад со скоростью – 60 км/ч. Необходимо рассчитать среднюю скорость автомобиля.

Средняя скорость () равна отношению пройденного пути (S) ко времени (T), затраченному на поездку. Тогда средняя скорость () равна

.

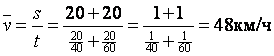В этом случае была использована средняя гармоническая простая.

Пример 2. Автомобиль в течение первого часа едет по трассе со скоростью 40 км/ч, а в течение второго часа – скоростью 60 км/ч. Найти среднюю скорость автомобиля.

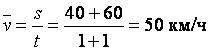
В данном случае использована средняя арифметическая простая.

Таким образом, эти два примера еще раз наглядно демонстрируют, что выбор той или иной формы средней зависит от имеющихся исходных данных.

Средняя гармоническая – это превращенная форма средней арифметической, когда частоты Fi не заданы (не известны), а известен сложный показатель Qi=Xi×Fi. Тогда Fi =Qi/Xi×и

.

Средняя гармоническая взвешенная находит более широкое применение в статистической практике по сравнению с простой. Использование средней гармонической целесообразно и обосновано для всех показателей интенсивности: цена, скорость, производительность труда, плотность населения и т. п.

4. Средняя геометрическая.

Средняя геометрическая простая

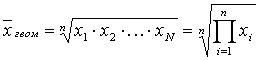. (3.5)

Средняя геометрическая взвешенная

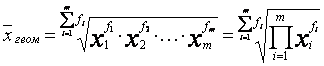. (3.6)

Средняя геометрическая обычно применяется в тех случаях, когда варианты ряда представлены относительными показателями динамики. Эта средняя выражает, как правило, средний темп относительного роста или спала.

Пример. Темп роста цен в январе – 105%, в феврале – 98% и в марте – 112%. Найти средний темп роста цен в I квартале.

Используем среднюю геометрическую простую

.

E При выполнении расчетов на калькуляторе более удобно использовать следующий вариант этой формулы

.

5. Средние степенные.

Все рассмотренные выше средние величины являются частным случаем Степенной средней.

Простая степенная средняя

. (3.7)

Взвешенная степенная средняя

. (3.8)

При K= –1 получаем среднюю гармоническую, при K=1 – среднюю арифметическую, при K=2 – среднюю квадратическую, при K=3 – среднюю кубическую и т. д.

Если вычислять степенную среднюю по основе одних и тех же исходных данных, то можно убедиться, что с ростом K значение степенной возрастает, т. е. справедливо Правило мажоритарности средних

.

< Предыдущая		Следующая >