13.01. Асимптоты

Асимптоты

Понятие асимптот, как уже отмечено выше, вводится для кривых, ветви которых уходят в бесконечность. Это может иметь место, когда функция неограничена или задана на неограниченном промежутке.

Прямая x = a называется вертикальной асимптотой графика функции y =, если хотя бы один из односторонних пределов

Равен или .

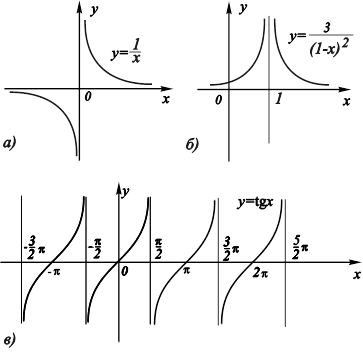
Например, график функции имеет вертикальную асимптоту, совпадающую с осью 0y (рис. 11.22, A), график функции имеет вертикальную асимптоту x = 1 (рис. 11.22, Б), а график функции имеет бесконечное число асимптот (рис. 11.22, В).

Прямая y = b называется горизонтальной асимптотой графика функции , если

.

Рис. 11.22. График некоторых функций, имеющих Вертикальные асимптоты.

 

Например, график функции y = arctgx имеет две горизонтальные асимптоты и (рис.11.23, А), так как

.

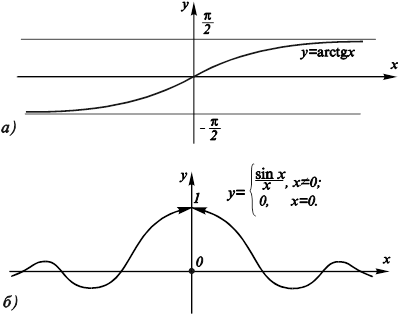
График функции

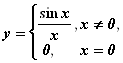
Имеет одну горизонтальную асимптоту y = 0 (рис. 11.23, Б), так как

.

Рис. 11.23. Графики некоторых функций, имеющих горизонтальные асимптоты.

 

Такую же асимптоту имеет уже рассмотренный график функции .

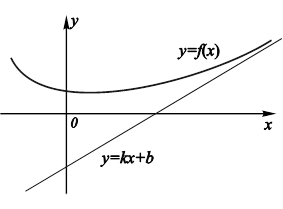
Прямая y = kx+b называется наклонной асимптотой графика функции (рис.11.24), если

. (11.17)

Определим коэффициенты k и b наклонной асимптоты. Разделим равенство (11.17) на X:

.

Рис. 11.24. Наклонная асимптота y = kx+b к графику Функции .

 

Отсюда следует, что

. (11.18)

Зная k, из (11.17) получим:

. (11.19)

При k = 0 будем иметь горизонтальную асимптоту, она является частным случаем наклонной асимптоты.

< Предыдущая		Следующая >