13.02. План исследования функции и построения графика

План исследования функции и построения графика

Область определения функции.

Четность функции, ее периодичность.

Непрерывность функции, точки разрыва.

Точки пересечения графика с осями координат.

Точки экстремума и экстремальные значения.

Интервалы возрастания и убывания функции.

Точки перегиба.

Участки выпуклости и вогнутости графика.

Асимптоты.

В ходе построения графика по мере необходимости можно получить дополнительный ряд значений функции при некоторых частных значениях аргумента, то есть получить дополнительно еще ряд точек графика. Порядок, указанный данной схемой построения графика можно менять.

В качестве примера исследуем функцию и построим ее график.

Область определения функции D(y) = R.

Функция нечетна, не является периодической.

Функция всюду непрерывна.

График функции проходит через начало координат.

.

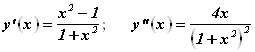Приравнивая производную нулю, находим точки, подозрительные на экстремум:

.

Используя вторую производную, определяем, что . Следовательно при функция имеет максимум

.

При функция имеет минимум

.

6. Функция возрастает в промежутках и , убывает в .

7. Исследуя знак второй производной, заключаем: в – график функции является выпуклым, а в – вогнутым.

8. Начало координат является точкой перегиба.

9. Находим наклонные асимптоты:

;

;

;

.

Получаем, что и – наклонные асимптоты.

Проведенное исследование позволяет построить график функции.

Рис. 11.25. График функции .

 

< Предыдущая		Следующая >