12.04. Исследование функции с помощью второй производной
Исследование функции с помощью второй производной
Вторая производная функции, если она существует, может быть так же эффективно использована для исследования на экстремум, определения промежутков выпуклости и вогнутости ее графика, отыскания точек перегиба.
ТЕОРЕМА 1 (ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА). Если для функции ![]() в точке
в точке ![]() производная
производная ![]() , А в ее окрестности
, А в ее окрестности ![]() непрерывна, причем
непрерывна, причем ![]()
![]() , то эта точка является точкой ее максимума (минимума).
, то эта точка является точкой ее максимума (минимума).
ДОКАЗАТЕЛЬСТВО.
Пусть в точке с выполняется равенство
![]()
И имеет место неравенство
![]()
Будучи непрерывной, вторая производная сохраняет свой знак при х, Близких к с. Поэтому для этих x
![]()
Но вторая производная функции есть производная от первой производной
![]()
|
Рис. 11.17. Возможное взаимное расположение графиков функций Максимума.
|
|
Это условие является достаточным признаком для существования экстремума, но не является необходимым. Почему? |
Следовательно, ![]() есть функция убывающая. По условию теоремы,
есть функция убывающая. По условию теоремы, ![]() . Это означает, что
. Это означает, что ![]() левее точки с Положительна, а правее – отрицательна. Переходя к самой функции
левее точки с Положительна, а правее – отрицательна. Переходя к самой функции ![]() , можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций
, можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций ![]() ,
, ![]() И
И ![]() в окрестности точки с.
в окрестности точки с.
Данная теорема может оказаться удобной, когда знак ![]() определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда
определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда ![]() не существует.
не существует.
Сформулируем без доказательства некоторое обобщение данной теоремы для случая, когда функция имеет производные порядка ![]() .
.
ТЕОРЕМА 2. Если функция ![]() в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем
в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем ![]() то при четном (n+1) функция
то при четном (n+1) функция ![]() имеет максимум, если
имеет максимум, если ![]() и минимум, если
и минимум, если ![]() .
.
Рассмотрим примеры.
Исследуем на экстремум функцию
![]()
Находим первую производную:
![]()
И приравниваем ее к нулю:
![]() .
.
Получаем, что x = 0 – Точка, подозрительная на экстремум.
![]()
![]()
Следовательно, в этой точке функция имеет максимум:
![]()
Рассмотрим теперь функцию
![]()
Ее первая производная
![]()
Также обращается в нуль при ![]() .
.
Легко обнаружить, что ![]() , так как
, так как
![]()
Однако по теореме 2 имеем:
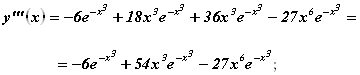
![]()
Следовательно, функция ![]() при
при ![]() Экстремума не имеет.
Экстремума не имеет.
Отсутствие экстремума у данной функции легко установить и без применения производной. Действительно, так как функция ![]() всюду возрастает, то функция
всюду возрастает, то функция
![]()
Убывает для ![]() , то есть экстремум отсутствует. Этот пример еще раз показывает, что при исследовании функций полезно использовать разнообразные приемы.
, то есть экстремум отсутствует. Этот пример еще раз показывает, что при исследовании функций полезно использовать разнообразные приемы.
Применим теперь вторую производную к исследованию на выпуклость и вогнутость графика функции.
Выше, в главе 3, мы определили эти понятия, связывая расположение кривой с расположением хорды, соединяющей две близкие точки этой кривой. Возможен и иной способ описания выпуклости и вогнутости кривой.
Будем называть график функции ![]() в точке
в точке ![]() вогнутым (выпуклым), если в окрестности точки М он расположен выше (ниже) касательной к кривой в этой точке (рис. 11.18).
вогнутым (выпуклым), если в окрестности точки М он расположен выше (ниже) касательной к кривой в этой точке (рис. 11.18).
|
А) расположение касательной к вогнутой кривой; Б) расположение касательной к выпуклой кривой. |
ТЕОРЕМА 3. Если функция ![]() в интервале
в интервале ![]() имеет положительную (отрицательную) вторую производную, то кривая на этом интервале вогнута (выпукла).
имеет положительную (отрицательную) вторую производную, то кривая на этом интервале вогнута (выпукла).
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольную точку с в интервале ![]() и покажем, что при
и покажем, что при ![]() точки графика функции, соответствующие значениям аргумента х, близлежащим к с, будут располагаться выше точек касательной к кривой
точки графика функции, соответствующие значениям аргумента х, близлежащим к с, будут располагаться выше точек касательной к кривой ![]() , Проведенной в точке
, Проведенной в точке ![]() (рис. 11.18). Уравнение касательной имеет вид:
(рис. 11.18). Уравнение касательной имеет вид:
![]()
Где ![]() – Ордината ее произвольной точки.
– Ордината ее произвольной точки.
Найдем разность ординат кривой ![]() и касательной к ней при одном и том же значении х, близком к с :
и касательной к ней при одном и том же значении х, близком к с :
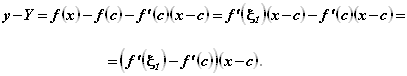
Здесь мы применили теорему Лагранжа к разности ![]() ,
, ![]()
К разности ![]() , рассматриваемой на отрезке
, рассматриваемой на отрезке ![]() , снова применим теорему Лагранжа. Получим:
, снова применим теорему Лагранжа. Получим:
![]()
Где ![]() .
.
Если ![]() , то
, то ![]() поэтому
поэтому
![]()
![]() ,
,
И при условии, что ![]() , имеем
, имеем
![]()
При ![]()
![]()
![]()
И так как ![]() , то
, то
![]()
Таким образом, любая точка кривой ![]() Лежит выше касательной, что и требовалось доказать.
Лежит выше касательной, что и требовалось доказать.
Аналогично доказывается выпуклость графика ![]() при
при
![]()
Точка ![]() графика функции
графика функции ![]() называется Точкой перегиба, если при переходе через нее кривая меняет свою выпуклость на вогнутость, или же наоборот. Последующие теоремы определяют критерии существования перегиба.
называется Точкой перегиба, если при переходе через нее кривая меняет свою выпуклость на вогнутость, или же наоборот. Последующие теоремы определяют критерии существования перегиба.
ТЕОРЕМА 4 (НЕОБХОДИМОЕ УСЛОВИЕ ПЕРЕГИБА). Если функция ![]() имеет в окрестности внутренней точки c области определения вторую непрерывную производную и точка
имеет в окрестности внутренней точки c области определения вторую непрерывную производную и точка ![]() , лежащая на графике функции, является точкой перегиба, то
, лежащая на графике функции, является точкой перегиба, то
![]()
ДОКАЗАТЕЛЬСТВО.
|
Может ли точка экстремума совпадать с точкой перегиба? |
Предположим противное:
![]()
|
Можно ли утверждать, что между двумя точками экстремума функции лежит хотя бы одна точка перегиба? |
В силу непрерывности ![]() найдется окрестность точки С, в которой
найдется окрестность точки С, в которой ![]() сохраняет знак, то есть график функции будет либо выпуклым, либо вогнутым, а потому точка
сохраняет знак, то есть график функции будет либо выпуклым, либо вогнутым, а потому точка ![]() не может быть точкой перегиба. Полученное противоречие доказывает утверждение теоремы
не может быть точкой перегиба. Полученное противоречие доказывает утверждение теоремы
|
Можно ли утверждать, что между двумя точками перегиба лежит хотя бы одна точка экстремума? |
![]() .
.
|
Графиком функции
|
Данная теорема позволяет отнести к точкам, где следует ожидать перегиб графика функции ![]() , те точки ее области определения, в которых
, те точки ее области определения, в которых ![]() Однако множество точек, подозрительных на перегиб, может быть расширено за счет тех, в которых
Однако множество точек, подозрительных на перегиб, может быть расширено за счет тех, в которых ![]() обращается в бесконечность или вовсе не существует. На рис. 11.19 указаны возможные случаи перегиба графика функции.
обращается в бесконечность или вовсе не существует. На рис. 11.19 указаны возможные случаи перегиба графика функции.
Укажем достаточные условия перегиба графика функции.
|
Функции |
ТЕОРЕМА 5 (ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА). Если при переходе через точку c, подозрительную на перегиб графика функции ![]() , вторая производная меняет знак, то точка графика
, вторая производная меняет знак, то точка графика ![]() есть точка перегиба.
есть точка перегиба.
ДОКАЗАТЕЛЬСТВО.
Из условия теоремы следует, что левее точки ![]() – кривая выпуклая (вогнутая), а правее ее – вогнутая (выпуклая). Значит,
– кривая выпуклая (вогнутая), а правее ее – вогнутая (выпуклая). Значит, ![]() – точка перегиба.
– точка перегиба.
Приведем без доказательства еще два признака перегиба графика функции.
ТЕОРЕМА 6. Если функция ![]() такова, что в точке с
такова, что в точке с ![]() , а
, а ![]() и конечна, то ее график в точке
и конечна, то ее график в точке ![]() имеет перегиб.
имеет перегиб.
Следующая теорема является более общей.
ТЕОРЕМА 7. Если функция ![]() в некоторой окрестности точки с имеет производную до (N+1)-го порядка, непрерывную в самой точке С, причем
в некоторой окрестности точки с имеет производную до (N+1)-го порядка, непрерывную в самой точке С, причем ![]() а
а ![]() , то при нечетном (n+1) График функции
, то при нечетном (n+1) График функции ![]() в точке
в точке ![]() будет иметь перегиб.
будет иметь перегиб.
Рассмотрим примеры.
Найдем точки перегиба функции ![]() .
.
Выше получено:
![]() .
.
Условие ![]() приводит нас к уравнению
приводит нас к уравнению
![]()
|
Можно ли с помощью второй производной исследовать функцию на монотонность? |
Которое имеет решения:
![]()
|
Какая из производных несет большую информацию о свойствах функции – первая или вторая? |
Исследуем эти точки, подозрительные на перегиб. Очевидно, что
![]() для
для ![]()
|
Есть ли функции, у которых: А) вторая производная изменяется, как и сама функция; Б) функция не совпадает с первой производной, но первая и вторая ее производные совпадают между собой? |
И ![]() ;
;
![]() для
для
![]() ,
,
|
Дана функция, являющаяся второй производной некоторой функции. Укажите функции, имеющие такую же вторую производную. |
Следовательно, для ![]() и
и ![]() кривая вогнута; для
кривая вогнута; для ![]() кривая выпукла, а точки графика
кривая выпукла, а точки графика ![]() и
и ![]() являются точками перегиба.
являются точками перегиба.
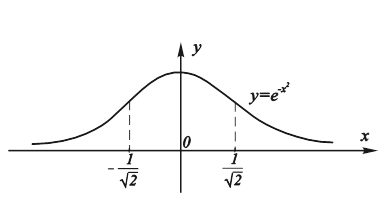
Данная функциональная зависимость встречается часто в теории вероятностей. Она известна под названием кривой Гаусса. Ее график изображен на рис. 11.20.
|
Рис. 11.20. График функции |
Вернемся теперь еще раз к функции ![]() .
.
Ее вторая производная имеет вид:
![]()
Условие
![]()
Приводит нас к уравнению
![]()
Которое имеет корни
![]()
Являющиеся абсциссами точек графика данной функции, подозрительных на перегиб.
Теорема 7 позволяет достаточно просто их исследовать. Имеем:
![]()
![]()
Следовательно, точка ![]() является точкой перегиба графика кривой
является точкой перегиба графика кривой ![]() .
.
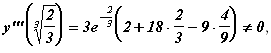
А потому и точка 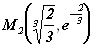 также является точкой перегиба. График данной функции схематично изображен на рис. 11.21.
также является точкой перегиба. График данной функции схематично изображен на рис. 11.21.
|
Рис. 11.21. График функции |
| < Предыдущая | Следующая > |
|---|
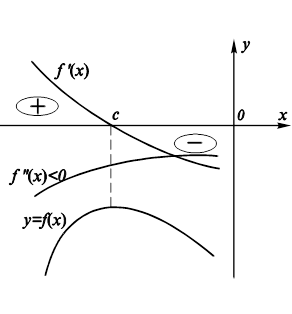
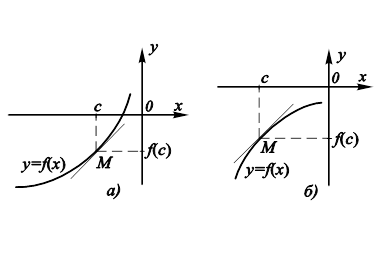 Рис. 11.18. Расположение кривой по отношению
Рис. 11.18. Расположение кривой по отношению 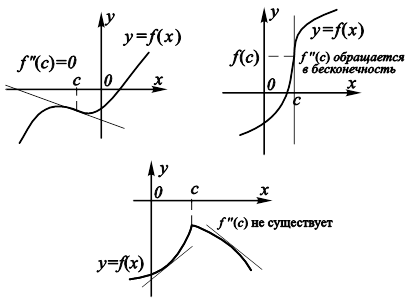 Рис. 11.19. Возможные случаи перегиба графика
Рис. 11.19. Возможные случаи перегиба графика