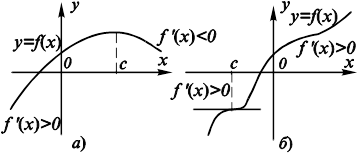12.03. Применение дифференциала к приближенным
По условию теоремы, ![]() , следовательно,
, следовательно, ![]() А значит,
А значит, ![]() – возрастающая функция, что и требовалось доказать.
– возрастающая функция, что и требовалось доказать.
Соответствующее утверждение имеет место и для отрицательной производной.
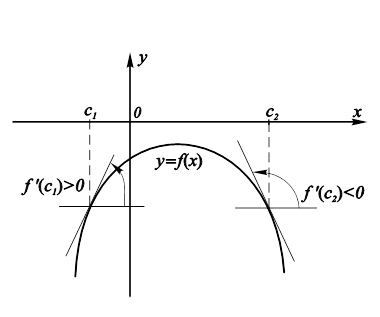
Доказанные теоремы позволяют связать возрастание и убывание функции со знаком производной. Геометрический смысл состоит в том, что при положительной производной касательная к графику функции образует острый угол с положительным направлением оси x и функция при этом возрастает, а для графика убывающей функции этот угол тупой и функция убывает (рис. 11.12).
|
Рис. 11.12. Связь возрастания и убывания функции Со знаком производной. |
ТЕОРЕМА 3 (НЕОБХОДИМОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА). Если функция ![]() имеет экстремум в некоторой точке С и в этой точке существует производная
имеет экстремум в некоторой точке С и в этой точке существует производная ![]() , то она равна нулю:
, то она равна нулю: ![]() .
.
ДОКАЗАТЕЛЬСТВО.
Пусть для определенности в точке c функция ![]() имеет максимум, тогда независимо от знака достаточно малых
имеет максимум, тогда независимо от знака достаточно малых ![]() будет иметь место неравенство
будет иметь место неравенство
![]()
По определению производной, в точке с имеем:
![]()
Но
![]() Для
Для ![]()
И
![]() Для
Для ![]() .
.
Следовательно, единственно возможным значением
![]()
Может быть нуль, то есть ![]() , что и требовалось доказать.
, что и требовалось доказать.
Подчеркнем, что данная теорема является всего лишь необходимым условием, но не достаточным. Это значит, что если в некоторой точке с
![]()
То вопрос о существовании экстремума остается открытым: он может быть или же не быть – нужны дополнительные исследования.
Если же
![]()
|
Пользуясь доказанной теоремой, сформулируйте достаточное условие обращения производной дифференцируемой функции в нуль. |
То этого уже достаточно, чтобы утверждать, что в точке с экстремума Нет (обратно–противоположная теорема эквивалентна прямой). В реальных условиях мы не знаем, имеет ли функция экстремум, поэтому, отыскивая корни уравнения
![]()
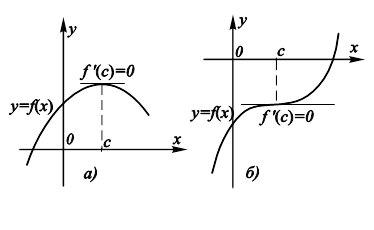
Мы находим лишь точки, подозрительные на экст-ремум (рис. 11.13). Требуются дополнительные исследования для установления его существования или отсутствия.
|
Рис. 11.13. Различные случаи поведения функции при равенстве нулю ее производной: а) наличие экстремума при равенстве нулю производной функции; б) отсутствие экстремума при равенстве нулю производной функции. |
|
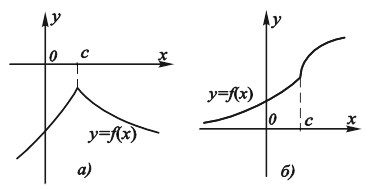
Рис. 11.14. Различные случаи поведения функции, Не имеющей производную в точке с: А) функция имеет экстремум; Б) функция экстремума не имеет. |
|
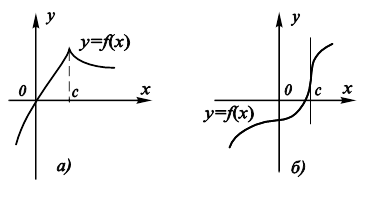
Рис. 11.15. Различные случаи поведения функции, имеющей бесконечную производную в точке с: А) функция имеет экстремум; Б) функция экстремума не имеет. |
Исчерпывают ли точки, подозрительные на экстремум, все возможные ситуации, при которых следует искать экстремум функции? Оказывается, нет. Точки, в которых производная функции не существует или обращается в бесконечность, тоже могут оказаться точками экстремума (рис. 11.14, 11.15).
Точки, в которых производная функции обращается в нуль, в бесконечность или же не существует, называются КРИТИЧЕСКИМИ. Их и следует выделить для продолжения исследования. Для этого рассмотрим достаточное условие существования экстремума функции.
ТЕОРЕМА 4 (ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА). Если функция ![]() непрерывна в интервале, содержащем критическую точку с, дифференцируема во всех точках этого промежутка, за исключением, быть может, самой точки с, и при переходе слева направо через критическую точку производная
непрерывна в интервале, содержащем критическую точку с, дифференцируема во всех точках этого промежутка, за исключением, быть может, самой точки с, и при переходе слева направо через критическую точку производная ![]() меняет знак с плюса (минуса) на минус (плюс), то в этой точке функция имеет максимум (минимум). Если смены знака производной
меняет знак с плюса (минуса) на минус (плюс), то в этой точке функция имеет максимум (минимум). Если смены знака производной ![]() не происходит, то точка с не является точкой экстремума.
не происходит, то точка с не является точкой экстремума.
ДОКАЗАТЕЛЬСТВО.
Пусть для определенности при переходе через точку с слева направо производная меняет знак с плюса на минус:
![]()
![]()
По теореме Лагранжа, на отрезке ![]() , принадлежащем данному интервалу,
, принадлежащем данному интервалу,
![]()
Для ![]() Имеем:
Имеем:
![]()
Поэтому
![]()
Или
![]() .
.
Для ![]() рассуждаем аналогично:
рассуждаем аналогично:
![]()
И также получим
![]()
Или
![]()
Это означает, что точка с – точка максимума. В случае минимума рассуждения аналогичны. Теорема доказана.
Если при переходе через точку с Не происходит смены знака производной, то, по теореме 2, функция ![]() сохраняет характер своей монотонности (при
сохраняет характер своей монотонности (при ![]() функция
функция ![]() Возрастает, а при
Возрастает, а при ![]() убывает). Следовательно, в точке с не может быть экстремума.
убывает). Следовательно, в точке с не может быть экстремума.
|
Рис. 11.16. Некоторые случаи применения первого Достаточного условия экстремума: А) максимум функции
Б) отсутствие экстремума функции
|
Достоинство данного признака существования экстремума состоит в том, что в самой точке с требуется лишь непрерывность функции, что существенно расширяет область его применения (рис. 11.16).
Его возможным недостатком могут быть трудности, возникающие при изучении знака первой производной слева и справа от точки с.
| < Предыдущая | Следующая > |
|---|