12.02. Дифференциал функции

Дифференциал функции

Пусть дана функция . Известно, что ее приращение в некоторой точке x0, вызванное приращением аргумента , может быть вычислено по формуле:

(11. 10)

Всегда ли удобно пользоваться ею? Можно ли приращение функции преобразовать так, чтобы выделить составляющие, которые в большей или меньшей степени отражали бы его структуру? Предыдущие рассуждения позволяют дать такую оценку.

Из определения производной получаем:

(11. 11)

Если некоторая функция имеет конечный предел, то по необходимому и достаточному условию существования предела она может быть представлена в виде:

(11. 12)

Где – бесконечно малая функция при , то есть

(11. 13)

Из равенства (6.12) получаем:

(11. 14)

Приращение функции состоит из двух слагаемых. Первое из них – – можно найти, вычислив и . Второе – – найти труднее, так как упомянутая выше теорема вовсе не указывает способа отыскания бесконечно малой функции . В случае необходимости ее можно найти как разность между приращением данной функции и первым слагаемым .

Рассмотрим пример. Пусть . Найдем первое и второе слагаемые в приращении функции, определяемые равенствами (11.14), когда , а DX = 3; 1; 0,1; -0,2.

Выполним преобразования:

; ;

При

Произведя расчеты, получим следующие результаты:

3	12	21	9
1	4	5	1
0,1	0,4	0,41	0,01
-0,2	-0,8	-0,76	0,04

Таблица № 12. Сравнение алгебраических слагаемых,

Входящих в приращение функции.

Попробуем уловить закономерности при , стремящемся к нулю. Во-первых, мало будут отличаться от нуля и DY, и , и . Во–Вторых, по мере приближения к нулю DX значимость первого слагаемого , его вклад в приращение функции возрастают, а второе слагаемое – , "теряет в весе", его роль снижается. В–Третьих, (это видно и без расчетов) изменяется линейно по отношению к DX, в то время как изменение величины этим свойством не обладает.

Обобщим результаты вычислительного эксперимента, проведя рассуждения в общем случае.

1. Оба слагаемых и в приращении функции являются бесконечно малыми:

2. Слагаемое является бесконечно малой функцией более высокого порядка малости, чем первое , при DX, стремящемся к нулю:

Так как функция бесконечно мала при DX, стремящемся к нулю, а ограничена ().

Это означает, что при DX, стремящемся к нулю, основная часть приращения функции приходится на первое слагаемое .

3. Независимо от вида функции и величины ее приращения, слагаемое всегда линейно относительно DX.

Проведенный анализ приращения функции, представленного равенством (11.14), указывает на особую роль в нем первого слагаемого.

Есть ли такая функция, для которой второе слагаемое : А) линейно по отношению к ? Б) тождественно равно нулю?

Линейная по отношению к приращению аргумента часть приращения функции называется ДИФФЕРЕНЦИАЛОМ функ-ции и обозначается:

(11. 15)

В этой записи принято считать

DX = Dx.

Действительно, если дана функция

То

Но, с другой стороны, по определению дифференциала,

Поэтому

Таким образом, дифференциал аргумента функции равен его приращению. Это и дает возможность записать дифференциал функции в виде (11.15).

Рассмотрим геометрический и физический смысл дифференциала функции.

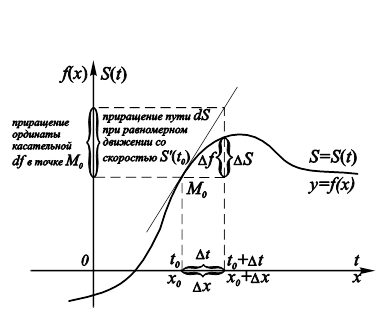
Пусть дана дифференцируемая функция , график которой изображен на рис. 11.4.

Рис. 11.4. Геометрический и физический смысл Дифференциала.

 

Из рис. 11.4 следует, что дифференциал геометрически означает приращение ординаты касательной к кривой в точке , вызванное приращением аргумента :

Приведите примеры функций, отражающих различные физические процессы, и укажите физический смысл их дифференциала в некоторой точке области определения.

Где J – угол, который образует касательная к кривой в точке .

Если же данная кривая – график функции пути S Материальной точки от времени , то величина – Приращение пути за время в предположении, что, начиная с момента времени , материальная точка движется равномерно со скоростью , которую она имела в начальный момент времени :

.

< Предыдущая		Следующая >