12.01. Дифференцирование функции, заданной неявно
Функциональная зависимость
Является явной, так как закон f прямо указывает каждому значению X Определенное значение Y, которое, в принципе, может быть найдено. Иногда этот закон, связывающий элементы множеств X и Y, имеет совершенно иную природу. Например, можно ли считать, что равенство
(11. 7)
Определяет функцию? При отрицательных a ни для какого x нельзя найти y, удовлетворяющие данному равенству. Если A = 0, то лишь для X = 0 можно указать Y = 0. Пусть теперь A > 0. Тогда возникает другая проблема: для любого 
находится сразу два значения y:
(11. 8)
Равенство (11.7) поэтому не определяет функцию. Но если ограничимся значениями 
, то есть
,
То получим функцию, графиком которой является верхняя часть окружности
.
Если в общем случае уравнение
(11. 9)
Задает функцию 
от аргумента 
, то говорят о ее неявном задании. Например, равенство
Задает неявно функцию 
. А задает ли функцию уравнение
,
Так легко сказать нельзя. В дальнейшем будет доказана теорема, определяющая критерий существования функции по ее неявному заданию (11.9). Но даже если (11.9) и задает неявную функцию, то ее дифференцирование может вызвать трудности, так как явное задание для нее не всегда находится просто. Оказывается, эта проблема преодолима: Не отыскивая саму функцию, удается получить ее производную. Для этого необходимо продифференцировать равенство (11.9), полагая y функцией аргумента x. Рассмотрим пример. Найдем 
, если
|
Данный пример может быть решен иначе: легко найдется x Как функция от y в явном виде, далее следует определить |
и по формуле дифференцирования обратной функции найти Дифференцируя левую и правую части по x, получим:
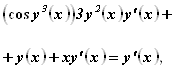
Отсюда
| < Предыдущая | Следующая > |
|---|
