11.4. Логарифмическое дифференцирование

Логарифмическое дифференцирование

Знание формул дифференцирования основных элементарных функций не всегда позволяет успешно находить производные более сложных функций. Например, для функции

, (11. 5)

Не применима ни одна из полученных формул.

Однако существует прием, который дает возможность преодолеть имеющуюся трудность. Прологарифмируем обе части равенства (11.5):

Возьмем производную от обеих частей, не забывая, что есть функция от X:

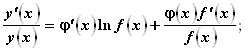
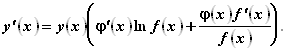
В итоге получим:

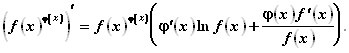
Данный метод успешно находит применение и тогда, когда функция представляет собой произведение большого числа сомножителей или является дробью, числитель и знаменатель которой состоят из ряда сомножителей.

Например, найдем производную функции

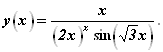
Вначале логарифмируем имеющееся равенство:

Затем выполняем дифференцирование:

Окончательно получаем:

< Предыдущая		Следующая >