11.3. Дифференцирование элементарных функций

Дифференцирование элементарных функций

Знание производных элементарных функций и правил дифференцирования позволяет выполнять эту операцию в конкретных случаях. Выведем соответствующие формулы:

1. (=const).

Воспользуемся определением производной:

.

Итак, .

2. – степенная функция (где – действительное число).

Дадим аргументу Приращение . Тогда

,

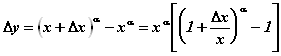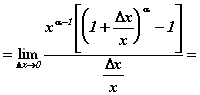
Где

Здесь мы воспользовались эквивалентностью (глава 9):

Таким образом,

В частности, по этой формуле будем иметь:

3. – логарифмическая функция.

Рассмотрим приращение функции , вызванное приращением аргумента в точке X:

.

По определению производной получим:

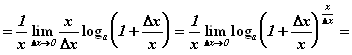
Где

Таким образом,

В частности,

4. – показательная функция.

Воспользуемся связью производных прямой и обратной функций:

Но из cоотношения следует, что

Значит,

Поэтому

Итак,

Интересен факт:

При каждом значении X скорость изменения функции y= совпадает с ее значением в данной точке. Это уже отмечалось при рассмотрении второго замечательного предела. Другой такой функции не существует.

5. Тригонометрические функции:

.

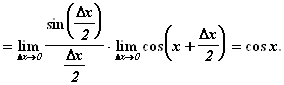
Итак, воспользовавшись первым замечательным пределом и непрерывностью функции , имеем:

Аналогично рассуждая, получим:

Правило дифференцирования дроби дает:

Рабочая формула принимает вид:

Проводя аналогичные преобразования, получим:

Найдем производные обратных тригонометрических функций:

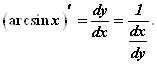
Так как

То

Перед знаком корня берем знак плюс, так как функция принимает значения для которых неотрицателен. Поэтому

Постройте графики некоторых функций и их производных в соответствующих областях определения. Существуют ли какие-то геометрические закономерности, вытекающие из взаимного расположения графиков?

Аналогично:

< Предыдущая		Следующая >