11.2. Свойства дифференцируемых функций

Свойства дифференцируемых функций

Будет ли функция иметь предел в точке, в которой существует ее производная? Будет ли непрерывной дифференцируемая функция? Эти вопросы возникают сразу же, потому что и понятие производной, и понятие непрерывности имеют общую первооснову – понятие предела.

ТЕОРЕМА 1. Если функция имеет производную на множестве X, то она непрерывна на этом множестве.

ДОКАЗАТЕЛЬСТВО.

Из условия теоремы следует, что отношение имеет конечный предел для любого X из множества X при , то есть:

По теореме, определяющей необходимое и достаточное условие существования предела, будем иметь:

Где – бесконечно малая функция при , стремящемся к нулю.

Находим приращение функции:

Оно складывается из двух бесконечно малых функций при , поэтому их сумма бесконечно мала, что и доказывает непрерывность функции .

Дифференцируемая функция непрерывна, значит, она имеет и предел в соответствующих точках.

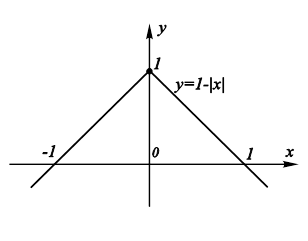
Рис. 11.2. Пример функции, недифференцируемой В отдельной точке.

Если непрерывная функция не имеет производную в некоторой точке, то можно ли эту функцию переопределить в этой точке так, чтобы она стала дифференцируемой?

Непрерывность функции является, однако, лишь необходимым, но не достаточным условием ее дифференцируемости. Например, рассмотрим функцию (рис. 11.2). Она может быть представлена в виде

Дайте определение бесконечной производной. Изобразите схематично графики непрерывных функций, имеющих бесконечную производную.

Если взять приращение аргумента в окрестности нуля

Может ли функция, у которой производная обращается в бесконечность, иметь в этой точке: А) устранимый разрыв; Б) разрыв первого рода; В) разрыв второго рода?

То слева от этой точки

А справа –

Если производная функции конечна для , то может ли сама функция быть бесконечно большой в этой точке?

При как слева, так и справа от точки 0, , то есть, непрерывна в нуле, однако

Это означает, что

Не существует, следовательно, при эта функция не является дифференцируемой.

Докажем теорему, позволяющую обосновать вычисление производных суммы, разности, произведения и частного двух функций.

ТЕОРЕМА 2. Если и дифференцируемы на множестве X, то производная суммы (разности) функций равна сумме (разности) их производных

(11. 1)

Производная произведения двух функций равна сумме произведений производной первой из них на вторую функцию, и первой функции на производную второй функции.

(11. 2)

Производная частного равна дроби, числитель которой есть разность произведений производной делимого на делитель и производной делителя на делимое, а знаменатель есть квадрат делителя.

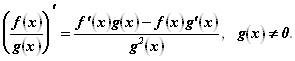(11. 3)

ДОКАЗАТЕЛЬСТВО.

Можно ли представить дифференцируемую функцию в виде суммы двух недифференцируемых?

Пусть аргумент x получает приращение . Тогда функции и будут иметь приращения и соответственно. Пользуясь определением производной, находим:

То есть

Это правило позволяет в случае необходимости выносить числовой множитель за знак производной, разбивать функцию на слагаемые, если производная каждого из них существует. В частности, при и имеем:

Так как предел последнего слагаемого равен нулю, потому что

.

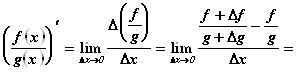
Почему при и ?

ТЕОРЕМА 3. Если для функции существует обратная функция и в рассматриваемой точке Х производная , то обратная функция в соответствующей точке дифференцируема, причем

ДОКАЗАТЕЛЬСТВО.

Придадим значению у приращение , тогда функция получит приращение , которое также отлично от нуля. Действительно, если бы , то , что невозможно. Следовательно, можно записать:

Пусть , тогда, в силу непрерывности обратной функции, и , поэтому

(11. 4)

Так как

ТЕОРЕМА 4. Если функция дифференцируема в точке T, а функция дифференцируема в точке X, то сложная функция дифференцируема в точке T, причем

ДОКАЗАТЕЛЬСТВО.

Дадим аргументу t приращение . Тогда функция Получит приращение . Оно, в свою очередь, вызовет приращение функции , равное . Согласно определению, при будем иметь:

Доказать, что производная четной функции – нечетна, а нечетной – четна.

Возможность перехода от предела при к пределу при оправдана тем, что дифференцируема, а значит, непрерывна, поэтому бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции . Это и доказывает теорему.

Рассмотренные свойства дифференцируемых функций приблизили нас к возможности непосредственного вычисления производных.

< Предыдущая		Следующая >