10.4. Равномерная непрерывность функции

Равномерная непрерывность функции

Пусть функция непрерывна во всех точках некоторого множества X. Для каждой точки а этого множества по заданному , характеризующему –Окрестность значения функции, мы находим каждый раз свою –Окрестность предельной точки a, позволяющую выделить значения , попадающие в –Окрестность точки . Переходя от одной точки к другой на множестве Х При одном и том же , мы будем находить в общем случае различные . А есть ли возможность по данному найти такое , которое было бы одним и тем же для всех ? 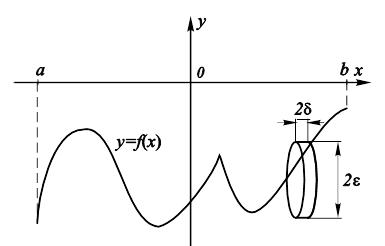Геометрически это означало бы, что через кривую может быть “протянуто” абсолютно тонкое кольцо диаметром и толщиной (рис. 10.9). В связи с этим вводится новое понятие.

Рис. 10.9. Геометрическая иллюстрация Равномерной непрерывности.

Будем говорить, что функция РАВНОМЕРНО НЕПРЕРЫВНА на множестве X, если для любого положительного числа найдется такое положительное число , единое для всех точек из этого множества, что для любой пары значений x, отстоящих друг от друга менее чем на , соответствующие значения функции будут отличаться друг от друга менее чем на . На языке логических символов это может быть записано следующим образом:

“ – Равномерно непрерывна” на

Долгое время в математике не удавалось сформулировать достаточные условия равномерной непрерывности функции. Лишь в середине XIX века Г. Кантор сформулировал простую и гениальную теорему.

ТЕОРЕМА КАНТОРА. Если функция непрерывна на отрезке , то она и равномерно непрерывна на этом отрезке.

< Предыдущая		Следующая >