10.3. Свойства непрерывных на отрезке функций
Свойства непрерывных на отрезке функций
Приведем без доказательства ряд теорем, относящихся к функциям, непрерывным на отрезке. Каждая из этих теорем имеет важное самостоятельное значение в математическом анализе. Несмотря на кажущуюся простоту и очевидность смысла данных теорем, доказать их оказалось делом нелегким. Это удалось осуществить сравнительно недавно – в XIX веке – выдающимся математикам: Вейерштрассу, Больцано, Коши. Современные ученые по достоинству оценили эти результаты и распространили их на наиболее сложные математические объекты исследования.
ТЕОРЕМА 1. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она достигает на нем своего наибольшего и наименьшего значений.
, то она достигает на нем своего наибольшего и наименьшего значений.
|
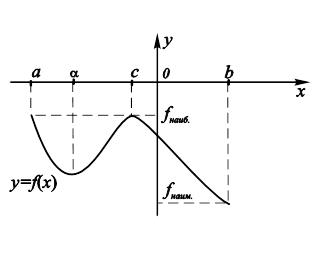
Рис. 10.4. Достижение непрерывной функцией своих |
Геометрический смысл данной теоремы иллюстрируется на рис. 10.4.
Наибольшее значение функции достигается сразу в двух точках области определения функции: на конце отрезка в точке ![]() и в его внутренней точке C, которая является ее максимумом. Наименьшее значение достигается не в точке минимума, а на конце B этого отрезка. Этот пример показывает, что минимум и максимум функции не всегда являются ее наименьшим и наибольшим значениями.
и в его внутренней точке C, которая является ее максимумом. Наименьшее значение достигается не в точке минимума, а на конце B этого отрезка. Этот пример показывает, что минимум и максимум функции не всегда являются ее наименьшим и наибольшим значениями.
Условия непрерывности функции ![]() и замкнутости промежутка, на котором она рассматривается, чрезвычайно важны. Невыполнение хотя бы одного из этих условий может нарушить справедливость теоремы. Например, функция
и замкнутости промежутка, на котором она рассматривается, чрезвычайно важны. Невыполнение хотя бы одного из этих условий может нарушить справедливость теоремы. Например, функция ![]() на отрезке [-3,1] не является непрерывной, она имеет при
на отрезке [-3,1] не является непрерывной, она имеет при ![]() бесконечный разрыв, поэтому указать для нее наибольшее и наименьшее значения невозможно. Более того, если непрерывную на отрезке
бесконечный разрыв, поэтому указать для нее наибольшее и наименьшее значения невозможно. Более того, если непрерывную на отрезке ![]() функцию переопределить всего лишь в одной (!) точке, то есть допустить устранимый разрыв, то сформулированная теорема может оказаться неверной. Например, функция
функцию переопределить всего лишь в одной (!) точке, то есть допустить устранимый разрыв, то сформулированная теорема может оказаться неверной. Например, функция ![]() на
на ![]() достигает наименьшее значение, равное нулю, при
достигает наименьшее значение, равное нулю, при ![]() и
и ![]() . Наибольшее значение, равное единице, достигается при
. Наибольшее значение, равное единице, достигается при ![]() . Однако стоит только переопределить эту функцию, положив, что
. Однако стоит только переопределить эту функцию, положив, что
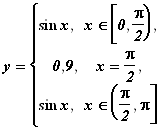
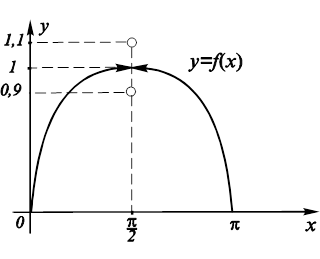
(рис. 10.5), как возможность достижения наибольшего значения новой функцией окажется неосуществима: как бы близко мы ни подошли к значению ![]() , функция будет принимать значения, сколь угодно близкие к единице, но не равные ей. Следует отметить, что если принять
, функция будет принимать значения, сколь угодно близкие к единице, но не равные ей. Следует отметить, что если принять ![]() , то утверждения теоремы 1 будут выполнены; то есть теорема 1 дает лишь достаточное условие достижения наибольшего и наименьшего значений функции.
, то утверждения теоремы 1 будут выполнены; то есть теорема 1 дает лишь достаточное условие достижения наибольшего и наименьшего значений функции.
|
Рис. 10.5. Существование глобального экстремума при нарушении одного из условий теоремы 1. |
Аналогично, если только допустить, что функция ![]() непрерывна не на отрезке
непрерывна не на отрезке ![]() , а, предположим, на полуинтервале, например,
, а, предположим, на полуинтервале, например, ![]() , то утверждение теоремы 1 может оказаться верным, а может и не быть таковым. Например, функция
, то утверждение теоремы 1 может оказаться верным, а может и не быть таковым. Например, функция ![]() на
на ![]() Достигает наименьшего значения – нуля, в точке
Достигает наименьшего значения – нуля, в точке ![]() , а наибольшего – единицы, когда
, а наибольшего – единицы, когда ![]() . Однако этой же функцией на
. Однако этой же функцией на ![]() наименьшее значение, равное нулю, при
наименьшее значение, равное нулю, при ![]() достигается, а наибольшее значение достигнуто быть не может.
достигается, а наибольшее значение достигнуто быть не может.
ТЕОРЕМА 2. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и принимает на его концах значения разных знаков, то в интервале
и принимает на его концах значения разных знаков, то в интервале ![]() найдется хотя бы одна такая точка c, в которой функция обратится в нуль:
найдется хотя бы одна такая точка c, в которой функция обратится в нуль:
![]() .
.
|
Сохранится ли утверждение теоремы, если функция имеет в некоторой точке отрезка устранимый разрыв? |
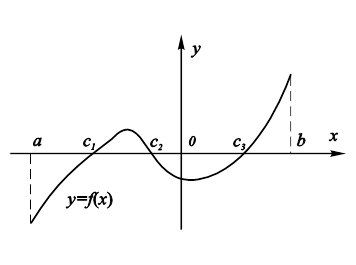
Геометрический смысл теоремы иллюстрируется рисунком 10.6. Функция, график которой здесь приведен, обращается в нуль даже в трех точках.
Данная теорема имеет важное значение для обоснования методов отыскания приближенных решений уравнения:
|
Рис. 10.6. Функция, удовлетворяющая условиям |
![]() .
.
Согласно ей, достаточно найти для непрерывной функции ![]() отрезки, на концах которых она имеет разные знаки, чтобы утверждать о существовании на них хотя бы одного действительного корня. Эта теорема могла бы иметь еще большее значение, если бы она указывала способ отыскания таких корней. В настоящее время математика богата самыми разнообразными методами приближенного решения уравнения
отрезки, на концах которых она имеет разные знаки, чтобы утверждать о существовании на них хотя бы одного действительного корня. Эта теорема могла бы иметь еще большее значение, если бы она указывала способ отыскания таких корней. В настоящее время математика богата самыми разнообразными методами приближенного решения уравнения ![]() . Все они основываются на теореме 2.
. Все они основываются на теореме 2.
Она важна также для обоснования метода интервалов при решении неравенств
![]() ,
,
Где ![]() – непрерывная функция.
– непрерывная функция.
Пусть ![]() ... – Корни уравнения
... – Корни уравнения
![]() .
.
Они разбивают область определения функции ![]() на отрезки так, что на их концах функция
на отрезки так, что на их концах функция ![]() обращается в нуль. Внутри этих отрезков функция сохраняет знак, так как в противном случае существовали бы внутренние точки промежутков, в которых функция обратилась бы в нуль, что невозможно: ведь все корни уравнения мы уже выделили. Если функция
обращается в нуль. Внутри этих отрезков функция сохраняет знак, так как в противном случае существовали бы внутренние точки промежутков, в которых функция обратилась бы в нуль, что невозможно: ведь все корни уравнения мы уже выделили. Если функция ![]() имеет разрывы, то при решении неравенства
имеет разрывы, то при решении неравенства ![]() их надо присоединить к корням уравнения. Взяв произвольную точку на каждом из полученных интервалов, мы определим на нем знак функции.
их надо присоединить к корням уравнения. Взяв произвольную точку на каждом из полученных интервалов, мы определим на нем знак функции.
Рассмотрим пример:
 .
.
Свяжем с данным неравенством функцию
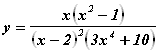 .
.
Отметим на числовой оси ![]() нули, точки разрыва функции, а также интервалы знакопостоянства (рис. 10.7).
нули, точки разрыва функции, а также интервалы знакопостоянства (рис. 10.7).
|
Рис. 10.7. Интервалы знакопостоянства данной функции. |
Отсюда видно, что решением неравенства будет
![]() .
.
ТЕОРЕМА 3. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и M – ее наименьшее значение, а М – наибольшее, то для любого числа
и M – ее наименьшее значение, а М – наибольшее, то для любого числа ![]() , лежавшего между m и М, найдется такое значение аргумента
, лежавшего между m и М, найдется такое значение аргумента ![]() , что
, что ![]() (рис. 10.8).
(рис. 10.8).
|
Рис. 10.8. Функция, удовлетворяющая условиям Теоремы 3. |
Смысл данной теоремы состоит в том, что непрерывная на отрезке функция принимает все значения, заключенные между ее наименьшим и наибольшим значениями, а потому ее называют теоремой о промежуточных значениях непрерывных функций.
| < Предыдущая | Следующая > |
|---|