09.6. Задачи и размышления
Задачи и размышления
1. Обязательно ли окрестность предельной точки a должна быть симметричной относительно нее? Возможны ли какие-то иные способы задания этой окрестности?
2. Каким образом в понятии “предел функции” используется определение понятия “функции”?
3. Доказать существование пределов:
А) ![]() в)
в) ![]()
Б) ![]() г)
г) ![]()
Построить графики соответствующих функций в окрестности предельной точки.
4. Доказать, что указанные пределы не существуют:
А) ![]() г)
г) ![]()
Б) ![]() д)
д) ![]()
В) ![]() е)
е) 
Построить графики данных функций в окрестности предельной точки.
5. Доказать, что числовая последовательность
![]()
Неограничена.
6. Доказать, что числовая последовательность
![]()
Стремится к бесконечности.
7. Доказать, что числовая последовательность

Имеет предел, равный нулю.
8. Совпадают ли понятия “числовая последова-тельность неограничена” и “числовая последовательность имеет бесконечный предел”?
9. Доказать, что
А) ![]() г)
г) ![]()
Б) ![]() д)
д) ![]()
В)![]() е)
е) 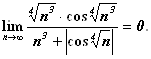
10. Последовательность
![]()
Является бесконечно большой. Следует ли из этого, что последовательности ![]() и
и ![]() бесконечно большие?
бесконечно большие?
11. Последовательность
![]()
Бесконечно малая. Может ли одна из последовательностей ![]() Или
Или ![]() быть бесконечно большой?
быть бесконечно большой?
12. Известно, что
![]()
Можно ли утверждать, что один из пределов
![]() и
и ![]() :
:
А)бесконечен; б)не существует; в)равен нулю?
13. Можно ли найти наибольший или же наименьший член числовой последовательности:
A)  б)
б) ![]()
14. Составьте алгоритм и программу для ЭВМ отыскания членов числовой последовательности, которые делятся на 3,5 и 8, но не делятся на 7 и 13.
15. Является ли числовая последовательность, сумма первых n членов которой равна:
А) ![]() б)
б) ![]() ,
,
Геометрической прогрессией?
16. Являются ли монотонными и ограниченными числовые последовательности:
А) ![]() д)
д) ![]()
Б) ![]() е)
е) 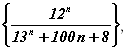
В) ![]() ж)
ж) 
Г) ![]()
17. Можно ли ожидать, что, начиная с некоторого номера n, все члены числовой последовательности
![]()
Попадут в интервал:
А) (2,6; 3,1); б) (2; 3); в)(3; 4)?
Обоснуйте вашу точку зрения.
18. С какого номера n все члены числовой последовательности

Окажутся в интервале:
А) (-2,5; 3,3),
Б) (2,95; 3,01)?
19. Найти формулу общего члена числовой последовательности Фибоначчи, заданной рекуррентными соотношениями:
![]()
Решение. Будем искать числовую последовательность ![]() , удовлетворяющую этим условиям, в виде
, удовлетворяющую этим условиям, в виде
![]()
Тогда
![]()
И соотношение
![]()
Принимает вид:
![]()
![]()
Каждая из последовательностей
![]() и
и ![]()
Удовлетворяет условию
![]()
Причем, как легко убедиться, даже последовательность
![]()
Где C1 и C2 - константы, тоже удовлетворяет ему. Воспользуемся возможностью выбора чисел C1 и C2 для удовлетворения условий:
![]()
Получим:

Решая систему, находим:
![]()
Формула общего члена приобретает вид:
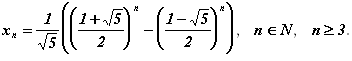
Первые члены последовательности Фибоначчи будут следующими (так называемые числа Фибоначчи):
![]()
Последовательность Фибоначчи очень любопытна: каждый ее член с номером, кратным трем, четный; каждый член с номером, кратным четырем, делится на 3; каждый пятнадцатый оканчивается нулем; соседние члены последовательности взаимно просты. Удивительных свойств этой последовательности чрезвычайно много. Найдите еще некоторые из них. Существуют объекты различной природы, при описании которых используются числа Фибоначчи. Знакомясь с литературой, отыщите такие объекты, изучите их математическое описание.
|
Вся математика – это, собственно, одно уравнение для других наук. Новалис |
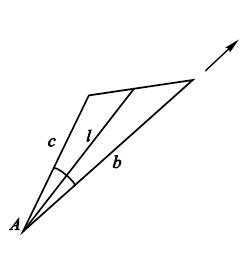
20. К чему стремится длина биссектрисы l треугольника, проведенной из вершины угла A, образованного сторонами b и c, когда ![]() (рис. 9.23), если угол A остается при этом неизменным?
(рис. 9.23), если угол A остается при этом неизменным?
|
Рис. 9.23. Геометрическая иллюстрация условия задачи. |
Изобразите графически это семейство треугольников и найдите зависимость ![]() . Есть ли возможность упростить эту зависимость путем использования эквивалентных функций? Задайте численные значения A и c, а также абсолютную погрешность результата DB и определите, с каких значений b оправдано применение упрощенной формулы.
. Есть ли возможность упростить эту зависимость путем использования эквивалентных функций? Задайте численные значения A и c, а также абсолютную погрешность результата DB и определите, с каких значений b оправдано применение упрощенной формулы.
21. К чему стремится биссектриса треугольника со сторонами a, b и c, проведенная к стороне c, при ![]() ?
?
|
Рис. 9.24. Геометрическая иллюстрация условия задачи. |
22. В основании четырехугольной пирамиды –прямоугольник со сторонами a и b. Один из двухгранных углов при ребре основания ![]() равен
равен ![]() . Двухгранные углы при ребрах, равных b, одинаковы. Сечение пирамиды, проходящее через ребро а, делит двухгранный угол
. Двухгранные углы при ребрах, равных b, одинаковы. Сечение пирамиды, проходящее через ребро а, делит двухгранный угол ![]() пополам. Найти площадь этого сечения, когда
пополам. Найти площадь этого сечения, когда ![]() при a = const и
при a = const и ![]() = const (рис.9.24).
= const (рис.9.24).
23. Приведите примеры, в которых вычисление предельных значений элементов каких-либо фигур требовало бы раскрытия неопределенностей и допускало бы упрощения с помощью эквивалентных функций.
24. Приведите примеры, в которых вычисление предельных значений физических характеристик каких-либо процессов или явлений требовало бы раскрытия неопределенностей и допускало бы упрощения с помощью эквивалентных функций.
25. Рассмотрим обозначенную в начале главы задачу о “превращении” квадратного уравнения
![]()
В линейное
![]()
Когда ![]() . Покажем, как происходит “исчезновение” одного из корней
. Покажем, как происходит “исчезновение” одного из корней
![]()
Квадратного уравнения и “превращение” другого в корень линейного уравнения
![]()
Действительно, пусть для определенности ![]() . Тогда при a, стремящемся к нулю, получим:
. Тогда при a, стремящемся к нулю, получим:
![]()
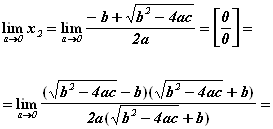
![]()
Если ![]()
![]() , то предельные значения
, то предельные значения ![]() и
и ![]() при
при ![]() меняются местами.
меняются местами.
Чтобы понять динамику процесса “перехода” квадратного уравнения в линейное, рассмотрим семейство парабол
![]()
При фиксированных b и c. Параметр a будем устремлять к нулю. Так как при ![]() и
и ![]() дискриминант квадратного трехчлена всегда положителен, то каждая парабола из этого семейства всегда пересекает ось x в двух точках. Кроме того, все эти параболы имеют общую точку М(0;c):
дискриминант квадратного трехчлена всегда положителен, то каждая парабола из этого семейства всегда пересекает ось x в двух точках. Кроме того, все эти параболы имеют общую точку М(0;c):
![]()
Известно, что координаты вершины параболы имеют вид:

Исключая параметр a, получим прямую, по которой будут перемещаться вершины парабол при заданных b и c и меняющихся a:
![]()
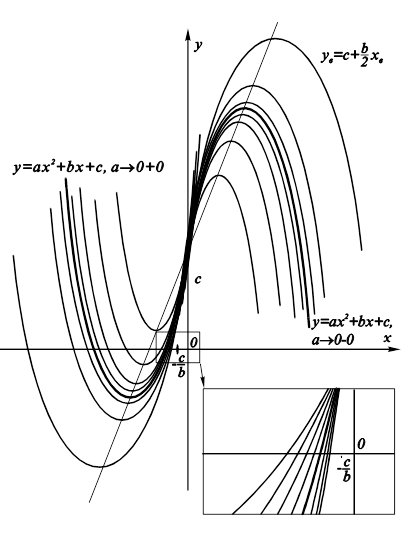
“Динамика” процесса изображена на рис.9.25.
|
Рис. 9.25. Трансформация графика квадратного трехчлена |
26. Исследовать корни квадратного трехчлена и его график при ![]()
![]()
![]()
![]() ;
; ![]()
27. Исследовать корни биквадратного уравнения ![]() при
при ![]()
![]()
![]()
![]()
![]() ;
; ![]()
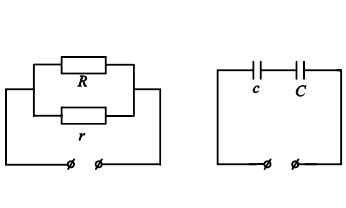
28. Параллельно соединенные электрические сопротивления r и R (рис.4.26,a) дают общее сопротивление в цепи
![]()
Последовательно соединенные конденсаторы c и C (рис.4.26,б) дают общую емкость в цепи переменного тока
![]()
|
А) б) Рис. 9.26. Аналогия электрических цепей: А) параллельное соединение сопротивлений; Б) последовательное соединение емкостей. |
Аналогия электрических цепей позволяет нам в случае необходимости заменять электрическую цепь, содержащую активные сопротивления, электрической цепью с реактивными сопротивлениями, и наоборот.
Мы видим аналогию этих процессов. Известны ли вам физические аналогии, подобные данной?
При неограниченном увеличении R общее сопротивление цепи будет стремиться к r.
Начиная с каких значений R можно считать ![]() , если абсолютная погрешность в определении
, если абсолютная погрешность в определении ![]() не должна превышать величины
не должна превышать величины ![]() ? Дайте трактовку этого результата для цепи, содержащей конденсаторы.
? Дайте трактовку этого результата для цепи, содержащей конденсаторы.
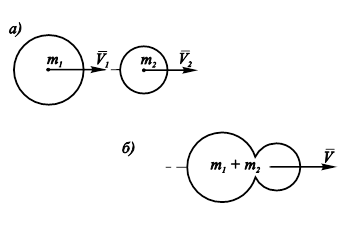
29. При неупругом соударении деформируемых тел, двигающихся в одном направлении (рис.9.27, a), скорость ![]() (рис.9.27, б) после соударения определяется по модулю формулой
(рис.9.27, б) после соударения определяется по модулю формулой
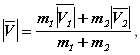
Где ![]() и
и ![]() - массы тел, а
- массы тел, а ![]() и
и ![]() - их скорости.
- их скорости.
|
Рис. 9.27. Соударение двух тел: A) положение тел до соударения; Б) положение тел после соударения. |
При увеличении массы второго тела ![]() результирующая скорость будет приближаться к
результирующая скорость будет приближаться к ![]() . Начиная с каких значений
. Начиная с каких значений ![]() , можно считать
, можно считать
![]()
С абсолютной погрешностью ![]() ?
?
Какая аналогия существует между вычислением скоростей в процессе соударения и нахождением центра тяжести двухмассовой системы? Приведите для конкретной системы соударяющихся тел аналог двухмассовой системы, позволяющий заменить задачу вычисления скоростей тела после соударения задачей нахождения координат центра тяжести соответствующей двухмассовой системы.
30. Английский математик Дж. Стирлинг в 1730 году нашел красивое представление для функции n!
![]()
При достаточно больших n. С каких n эта формула даст погрешность, не превосходящую 5%?
При решении физических задач довольно часто используются идеи симметрии, позволяющие (иногда весьма существенно) упростить расчеты.
Рассмотрим электрическую цепь, изображенную на рис.9.28,а. Найдем ее общее сопротивление между точками A и B, считая, что каждое сопротивление равно r.
В общем случае расчет таких цепей может быть произведен с помощью уравнений Кирхгофа. Однако, это трудоемкий путь решения. Из соображений симметрии ясно, что узлы 1,2,3 и 4,5,6 совершенно равноправны, поэтому токи, идущие по ветвям A–1, A–2 и A–3, одинаковы. Так как сопротивление этих ветвей одинаково, то одинаковы и потенциалы узлов 1,2,3. Аналогично можно утверждать, что эквивалентны узлы 4,5 и 6.
Сопротивление цепи не изменится, если эквивалентные узлы 1,2 и 3 соединить вместе. Можно соединить также и вторую тройку узлов 4,5 и 6. Получим цепь, состоящую из трех групп параллельно соединенных сопротивлений (рис. 9.28, б), которая без труда может быть упрощена до трех последовательно соединенных сопротивлений (рис. 9.28, в)
![]()
Отсюда общее сопротивление электрической цепи
![]() R.
R.
|
Рис. 9.28. Расчетная электрическая цепь A) данная электрическая цепь; Б) упрощенное представление электрической цепи; В) последующее упрощение электрической цепи. |
Электрическая схема на рис. 9.28, б подсказывает возможные пути использования предложенного метода. Например, идея упрощения электрической цепи из свойств симметрии сохранится, если блоки параллельно соединенных сопротивлений будут отличаться между собой своим сопротивлением, но внутри них сопротивления должны быть равны между собой.
31. Какие могут быть еще сделаны обобщения исходной электрической цепи, сохраняющие свойства симметрии и возможность выделения эквипотенциальных узлов? Будет ли при разных сопротивлениях электрическая цепь, изображенная на рис.9.28,б, эквивалентна данной? Какое сопротивление следует вставить между точками A и В, чтобы общее сопротивление цепи уменьшилось в два раза?
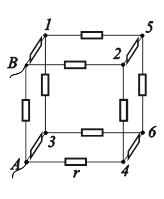
32. Рассмотрите “кубик” сопротивлений (рис.9.29), когда напряжение приложено к узлам A и B, с точки зрения возможных условий симметрии и найдите общее сопротивление цепи. Какие допустимы изменения сопротивлений, не нарушающие свойства симметрии?
|
Рис. 9.29. Другой вариант электрического нагружения кубика сопротивлений. |
33. Если дан “кубик” с равными сопротивлениями, то между какими его вершинами общее сопротивление цепи будет наибольшим и наименьшим?
В расчетах электрических цепей используются различные математические идеи. Одна из них – построение рекуррентных соотношений – Применяется тогда, когда задача допускает решение по шагам, причем на n-Ом шаге надо использовать результаты предшествующих шагов. Рекуррентные методы особенно удобны, когда электрическая схема имеет повторяющиеся структуры и число сопротивлений велико.
Рассмотрим конкретный пример. Пусть дана электрическая цепь, изображенная на рис. 9.30, а. Найдем сопротивление между точками A и B.
Чтобы выделить необходимые повторяющиеся структуры, представим данную электрическую цепь иначе (рис. 9.30, б). Повторяющаяся составляющая электрической схемы легко угадывается. Она изображена на рис. 9.30, в. Ее сопротивление ![]() вычисляется просто:
вычисляется просто:
![]()
|
Рис. 9.30. Упрощение электрической цепи Путем выделения повторяющихся структур: А) исходная расчетная схема; Б) другое представление электрической цепи; В) повторяющаяся структура электрической цепи; Г) упрощенная электрическая цепь; Д) завершающий этап упрощения электрической цепи. |
Это позволяет электрическую цепь упростить до вида, изображенного на рис. 9.30, г. В полученной цепи также можно обнаружить структуру, аналогичную уже рассмотренной (рис. 9.30, в).
Ее сопротивление –
![]()
На завершающем этапе упрощения получаем электрическую цепь, изображенную на рис. 9.30, д, и находим искомое сопротивление:
![]()
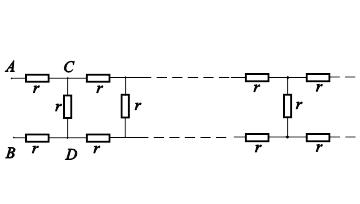
Если рассматривать теперь электрическую цепь (рис. 9.31), содержащую бесконечно много последовательно повторяющихся структур типа той, что изображена на рис. 9.30, в, то, упрощая ее справа налево, получим следующую числовую последовательность значений эквивалентных сопротивлений, соответствующих отбрасываемым в схеме частям:
![]() .
.
![]()
![]()
![]()
![]() .... .
.... .
|
Рис. 9.31. Электрическая цепь, содержащая бесконечно много повторяющихся структур. |
На ![]() -ом шаге эквивалентное сопротивление Rn может быть задано формулой:
-ом шаге эквивалентное сопротивление Rn может быть задано формулой:
![]()
![]()
Естественно возникает вопрос: а сходится ли числовая последовательность ![]() и каков ее предел? Попробуем ответить на первый вопрос, используя теорему Вейерштрасса. Исследуем ограниченность и монотонность данной последовательности.
и каков ее предел? Попробуем ответить на первый вопрос, используя теорему Вейерштрасса. Исследуем ограниченность и монотонность данной последовательности.
Действительно, так как r > 0 и для любого ![]() Справедливо
Справедливо
![]()
то числовая последовательность ограничена снизу числом r.
Кроме того,
![]() ,
,
Следовательно, числовая последовательность ограничена сверху числом 2r.
Таким образом,
![]()
Рассмотрим разность ![]() и попытаемся исследовать на монотонность числовой последовательности
и попытаемся исследовать на монотонность числовой последовательности ![]() .
.
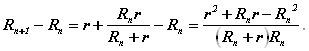
При изменении ![]() от r до 2r Имеем:
от r до 2r Имеем:
![]()
![]()
![]()
Но проводимые преобразования не позволяют судить о монотонности числовой последовательности ![]() . Здесь требуются более точные оценки. Если их не удается получить, то приходится ограничиваться правдоподобными рассуждениями: проведенные упрощения показывают, что на каждом новом шаге электрическая цепь сводится к двум параллельно соединенным сопротивлениям и одному сопротивлению, связанному с ним последовательно. Из физического смысла задачи следует существование предела
. Здесь требуются более точные оценки. Если их не удается получить, то приходится ограничиваться правдоподобными рассуждениями: проведенные упрощения показывают, что на каждом новом шаге электрическая цепь сводится к двум параллельно соединенным сопротивлениям и одному сопротивлению, связанному с ним последовательно. Из физического смысла задачи следует существование предела ![]() при
при ![]() . Поэтому, рассматривая соотношение
. Поэтому, рассматривая соотношение
![]()
Можно считать предел существующим и конечным:
![]()
Тогда для отыскания величины R получаем уравнение
![]()
Оно сводится к квадратному
![]()
Которое имеет один корень, удовлетворяющий физическому смыслу задачи,
![]()
Вычисления по рекуррентным формулам показывают, что значения ![]() с ростом n очень быстро приближаются к предельному значению.
с ростом n очень быстро приближаются к предельному значению.
Если известна абсолютная погрешность E, которая допускается при вычислении R, то, рассматривая разность
![]()
Или
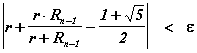 ,
,
Можно найти ![]() и далее тот номер n, с которого будет обеспечиваться данное неравенство.
и далее тот номер n, с которого будет обеспечиваться данное неравенство.
Для завершения решения задачи находим RAB, считая сопротивления R и r соединенными параллельно:
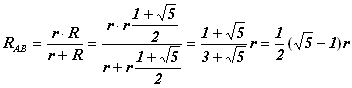 .
.
На практике не всегда удается найти предел числовой последовательности. В таком случае за его значение принимают значение его члена при достаточно большом номере N. Для этого есть убедительные Основания. Здесь полезно воспользоваться Критерием Коши: чтобы числовая последовательность ![]() была сходящейся, необходимо и достаточно, чтобы для любого положительного
была сходящейся, необходимо и достаточно, чтобы для любого положительного ![]() нашелся такой номер n0, что для всех
нашелся такой номер n0, что для всех ![]() и
и ![]() выполнялось бы неравенство
выполнялось бы неравенство ![]() . На языке кванторных операций это утверждение имеет вид:
. На языке кванторных операций это утверждение имеет вид:
![]()
Возможность по заданной абсолютной погрешности вычисления общего сопротивления R найти номер n0, то есть достаточное число повторяющихся структур электрической цепи, при которых эта погрешность выдерживается, очень важна для практики. Эта возможность позволяет избавить электрическую схему от излишних усложнений.
Возвращаясь к рассмотренной задаче, сравните между собой значения n при фиксированных r и e, с которых будут выполняться условия:
![]() и
и ![]() –
–
Полагая, что m = n–1, то есть сравнивая по модулю два рядом стоящих члена числовой последовательности {Rn}.
Просматривается ли в расчетах этой электрической цепи какая–то связь с числами Фибоначчи?
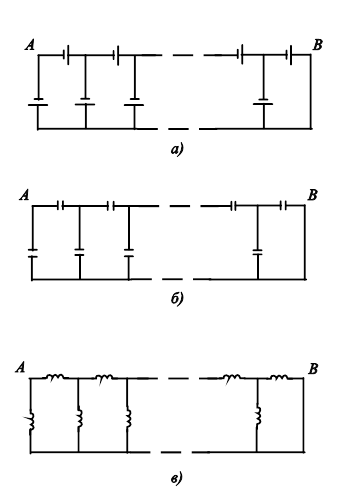
В какой мере можно использовать решение данной задачи для расчета между точками А и В:
А) электродвижущей силы батареи источников постоянного тока (рис.9.32, а);
|
Рис.9.32. Аналоги рассмотренной электрической цепи. |
Б) емкости батареи конденсаторов (рис.9.32,б) и индуктивностей (рис. 9.32,в) в цепях переменного тока?
Могут ли быть найдены механические и другие аналоги для данных электрических цепей?
Какую роль в данной задаче играют числа Фибоначчи?
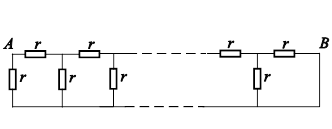
34. Дана бесконечная электрическая цепь (рис.9.33).
|
Рис. 9.33. Расчетная электрическая цепь. |
Сколькими звеньями в этой цепи можно ограничиться, чтобы абсолютная погрешность вычисления общего сопротивления R не превзошла величины ![]() ?
?
Найдите возможные аналоги для данной электрической цепи.
| < Предыдущая | Следующая > |
|---|